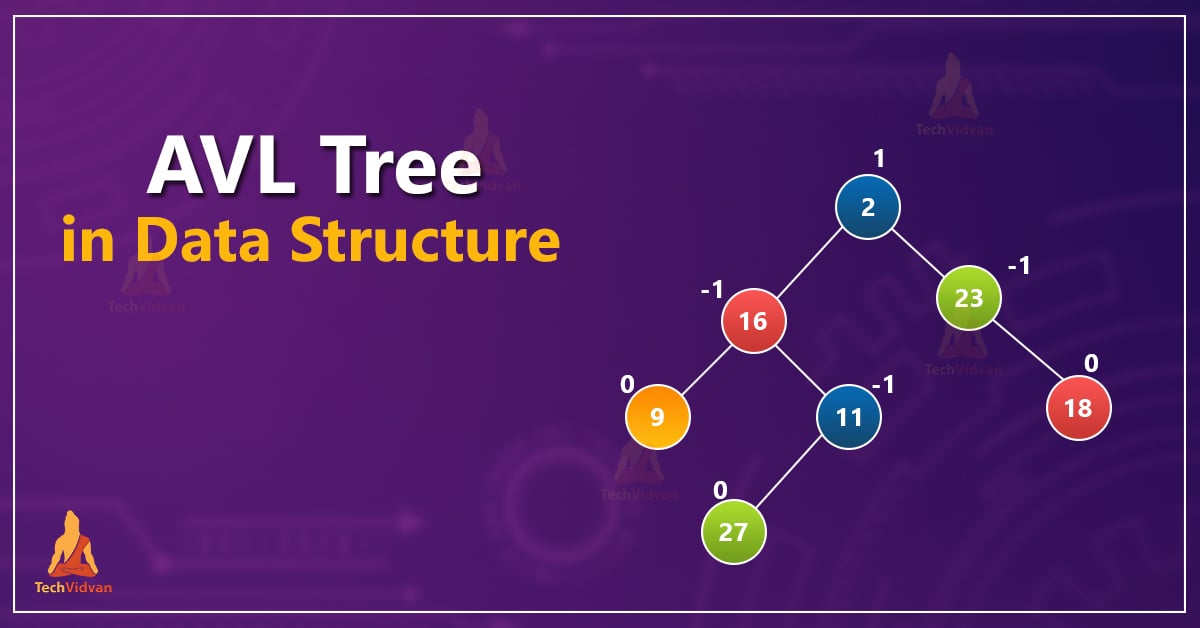
An AVL tree is a height-balanced binary search tree. The AVL tree is named after its inventors: Adelson-Velsky and Landis. In an AVL tree, the heights of the two-child subtrees can differ by utmost 1. AVL trees are based on a balancing factor. An AVL tree must have a balancing factor of either -1, 0 or 1. If the balancing factor is something else, we need to rebalance the AVL tree until the balancing factor is either 0, -1 or 1.
Balancing Factor:
The difference between the height of the left subtree and the height of the right subtree is known as the balancing factor. In an AVL tree, each node maintains extra information about the balancing factor. In an AVL tree, the balancing factor must be 0, -1 or 1. The balancing factor helps to maintain the self-balancing property of the AVL tree.
Thus, Balancing factor = (height of left subtree) – (height of right subtree)
Or, Balancing factor = (height of right subtree) – (height of left subtree)
Thus, for a tree to be an AVL tree:
- It must be a binary search tree.
- Its balancing factor must be -1, 0 or 1.
The following diagram depicts a height-balanced AVL tree.
Why AVL Trees:
For a binary search tree, the time taken to for execution is O(h) and in AVL trees, this height is balanced. In a simple binary search tree, the height could reach up to O(n) whenever the search tree is skewed. But, in the case of AVL trees, skewness can never exist and so the complexity is always the O(log n).
Operations on AVL trees:
We can perform the following operations on an AVL tree:
1. AVL rotations
2. Searching
3. Insertion
4. Deletion
AVL Rotations:
An AVL tree performs four kinds of rotations to balance itself. These four rotations are:
a. AVL Left Rotation:
If a node in a tree becomes unbalanced due to the nodes of the right subtree, then we left-rotate the parent node to balance the tree. Left rotation is performed on a right-skewed binary search tree.
b. AVL Right Rotation:
If a tree is not height-balanced due to the left subtree, we rotate it in the rightward direction to balance it. Right rotation is performed from left-skewed binary search trees.
c. AVL Left-right Rotation:
It comprises two rotations to balance the subtree- a left rotation and a right rotation. Consider the following example of a skewed binary search tree:
Here, R is unbalanced with a balancing factor of 2. Thus, we need to balance it. To balance it, we will first perform left rotation on the subtree of R. This will make it completely left-skewed. Then, we will perform the right rotation on this tree and get the balanced tree.
d. AVL Right-left Rotation:
It comprises a right rotation and a left rotation to balance the height of the tree.
Here, P is unbalanced. To balance it, we first need to right rotate the tree such that it becomes completely right-skewed. Then, we will perform left rotation on it to balance the tree.
Insertion in AVL Tree:
Insertion in an AVL tree requires that nodes must be added to the AVL tree such that the balancing factor remains 0, 1 or -1. If the balancing factor is something else, we need to balance the node by performing rotations.
If we need to insert a leaf node in an AVL tree, its balancing factor is always 0. So, we don’t need to rebalance it. If we are inserting an internal node, we need to take care of the balancing factor.
For example, consider the following AVL tree and make sure that it is height-balanced.
Suppose we want to insert 42 in this tree. 42>20, therefore, it will be in the right subtree. The next node is 50 and 50>42, therefore, 42 will be in the left subtree of 50. Again, 32<42, so 42 will be on the right subtree of 32. The next node we encounter is 46 and 46>42, thus, the final place of 42 will be on the left of 46 as shown:
However, on inserting 42, the balancing factor of 32 becomes -2 and the balancing factor of 50 becomes 2. Thus, the insertion of a new node has disrupted the balancing factor of the tree. This imbalance is due to 3 nodes- 32, 46 and 42.
If we are able to balance them, we will balance the whole tree. To balance these 3 nodes, we will first perform a right rotation as shown:
Then, we will perform a left rotation.
Finally, after performing these two rotations, we will get the balanced tree.
Deletion in AVL Trees:
The deletion works in a similar manner. First, we need to find the node to be deleted. Then, we delete the node and if the tree loses balance on removing the need, then we need to rebalance it. We know that deletion of any node in any binary search tree is handled in three different cases:
1. The node is a leaf node
2. The node is an internal node having one child
3. The node is an internal node having two child nodes
Consider the following tree:
Suppose we wish to delete 50.
On deleting 50, 60 will be replaced by 50 and 50 will be deleted as shown:
Now, the tree has become unbalanced due to the nodes: 60, 42 and 32.
This is a left-skewed tree so will perform right rotation to balance it. Thus, after performing the right rotation, the tree will become as follows:
This is a height-balanced AVL tree.
AVL Tree Implementation in C:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int key;
struct Node *left_child;
struct Node *right_child;
int height;
};
int Max(int a, int b);
int height(struct Node *N) {
if (N == NULL)
return 0;
return N->height;
}
int Max(int num1, int num2) {
return (num1 > num2) ? num1 : num2;
}
struct Node *new_node(int key) {
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->key = key;
node->left_child = NULL;
node->right_child = NULL;
node->height = 1;
return (node);
}
struct Node *right_rotate(struct Node *b) {
struct Node *a = b->left_child;
struct Node *t = a->right_rotate;
a->right_child = b;
b->left_child = t;
b->height = Max(height(b->left_child), height(b->right_child)) + 1;
a->height = Max(height(a->left_child), height(a->right_child)) + 1;
return a;
}
struct Node *left_rotate(struct Node *a) {
struct Node *b = a->right_child;
struct Node *t = b->left_child;
b->left_child = a;
a->right_child = t;
a->height = Max(height(a->left_child), height(a->right_child)) + 1;
b->height = Max(height(b->left_child), height(b->right_child)) + 1;
return b;
}
int get_balancing_factor(struct Node *N) {
if (N == NULL)
return 0;
return height(N->left_child) - height(N->right_child);
}
struct Node *insert_node(struct Node *node, int key) {
if (node == NULL)
return (new_node(key));
if (key < node->key)
node->left_child = insert_node(node->left_child, key);
else if (key > node->key)
node->right_child = insert_node(node->right_child, key);
else
return node;
node->height = 1 + Max(height(node->left_child), height(node->right_child));
int balance = get_balancing_factor(node);
if (balance > 1 && key < node->left_child->key)
return right_rotate(node);
if (balance < -1 && key > node->right_rotate->key)
return left_rotate(node);
if (balance > 1 && key > node->left_child->key) {
node->left_child = left_rotate(node->left_child);
return right_rotate(node);
}
if (balance < -1 && key < node->right_child->key) {
node->right_child = right_rotate(node->right_child);
return left_rotate(node);
}
return node;
}
struct Node *min_value(struct Node *node) {
struct Node *current = node;
while (current->left_child != NULL)
current = current->left_child;
return current;
}
struct Node *delete_node(struct Node *root, int key) {
if (root == NULL)
return root;
if (key < root->key)
root->left_child = delete_node(root->left_child, key);
else if (key > root->key)
root->right_child = delete_node(root->right_child, key);
else {
if ((root->left_child == NULL) || (root->right_child == NULL)) {
struct Node *temp = root->left_child ? root->left_child : root->right_child;
if (temp == NULL) {
temp = root;
root = NULL;
}
else
*root = *temp;
free(temp);
}
else {
struct Node *temp = min_value(root->right_child);
root->key = temp->key;
root->right_child = delete_node(root->right_child, temp->key);
}
}
if (root == NULL)
return root;
root->height = 1 + Max(height(root->left_child), height(root->right_child));
int balance = get_balancing_factor(root);
if (balance > 1 && get_balancing_factor(root->left_child) >= 0)
return right_rotate(root);
if (balance > 1 && get_balancing_factor(root->left_child) < 0) {
root->left_child = left_rotate(root->left_child);
return right_rotate(root);
}
if (balance < -1 && get_balancing_factor(root->right_child) <= 0)
return left_rotate(root);
if (balance < -1 && get_balancing_factor(root->right_child) > 0) {
root->right_child = right_rotate(root->right_child);
return left_rotate(root);
}
return root;
}
void Display_preOrder(struct Node *root) {
if (root != NULL) {
printf("%d ", root->key);
Display_preOrder(root->left_child);
Display_preOrder(root->right_child);
}
}
int main() {
struct Node *root = NULL;
root = insert_node(root, 20);
root = insert_node(root, 10);
root = insert_node(root, 60);
root = insert_node(root, 8);
root = insert_node(root, 15);
root = insert_node(root, 42);
root = insert_node(root, 50);
root = insert_node(root, 32);
Display_preOrder(root);
root = delete_node(root, 50);
printf("\nAfter deletion: ");
Display_preOrder(root);
return 0;
}
Implementation of AVL Tree in C++:
#include <bits/stdc++.h>
struct Node {
int key;
struct Node *left_child;
struct Node *right_child;
int height;
};
int Max(int a, int b);
int height(struct Node *N) {
if (N == NULL)
return 0;
return N->height;
}
int Max(int num1, int num2) {
return (num1 > num2) ? num1 : num2;
}
struct Node *new_node(int key) {
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->key = key;
node->left_child = NULL;
node->right_child = NULL;
node->height = 1;
return (node);
}
struct Node *right_rotate(struct Node *b) {
struct Node *a = b->left_child;
struct Node *t = a->right_rotate;
a->right_child = b;
b->left_child = t;
b->height = Max(height(b->left_child), height(b->right_child)) + 1;
a->height = Max(height(a->left_child), height(a->right_child)) + 1;
return a;
}
struct Node *left_rotate(struct Node *a) {
struct Node *b = a->right_child;
struct Node *t = b->left_child;
b->left_child = a;
a->right_child = t;
a->height = Max(height(a->left_child), height(a->right_child)) + 1;
b->height = Max(height(b->left_child), height(b->right_child)) + 1;
return b;
}
int get_balancing_factor(struct Node *N) {
if (N == NULL)
return 0;
return height(N->left_child) - height(N->right_child);
}
struct Node *insert_node(struct Node *node, int key) {
if (node == NULL)
return (new_node(key));
if (key < node->key)
node->left_child = insert_node(node->left_child, key);
else if (key > node->key)
node->right_child = insert_node(node->right_child, key);
else
return node;
node->height = 1 + Max(height(node->left_child), height(node->right_child));
int balance = get_balancing_factor(node);
if (balance > 1 && key < node->left_child->key)
return right_rotate(node);
if (balance < -1 && key > node->right_rotate->key)
return left_rotate(node);
if (balance > 1 && key > node->left_child->key) {
node->left_child = left_rotate(node->left_child);
return right_rotate(node);
}
if (balance < -1 && key < node->right_child->key) {
node->right_child = right_rotate(node->right_child);
return left_rotate(node);
}
return node;
}
struct Node *min_value(struct Node *node) {
struct Node *current = node;
while (current->left_child != NULL)
current = current->left_child;
return current;
}
struct Node *delete_node(struct Node *root, int key) {
if (root == NULL)
return root;
if (key < root->key)
root->left_child = delete_node(root->left_child, key);
else if (key > root->key)
root->right_child = delete_node(root->right_child, key);
else {
if ((root->left_child == NULL) || (root->right_child == NULL)) {
struct Node *temp = root->left_child ? root->left_child : root->right_child;
if (temp == NULL) {
temp = root;
root = NULL;
}
else
*root = *temp;
free(temp);
}
else {
struct Node *temp = min_value(root->right_child);
root->key = temp->key;
root->right_child = delete_node(root->right_child, temp->key);
}
}
if (root == NULL)
return root;
root->height = 1 + Max(height(root->left_child), height(root->right_child));
int balance = get_balancing_factor(root);
if (balance > 1 && get_balancing_factor(root->left_child) >= 0)
return right_rotate(root);
if (balance > 1 && get_balancing_factor(root->left_child) < 0) {
root->left_child = left_rotate(root->left_child);
return right_rotate(root);
}
if (balance < -1 && get_balancing_factor(root->right_child) <= 0)
return left_rotate(root);
if (balance < -1 && get_balancing_factor(root->right_child) > 0) {
root->right_child = right_rotate(root->right_child);
return left_rotate(root);
}
return root;
}
void Display_preOrder(struct Node *root) {
if (root != NULL) {
cout<< root->key;
Display_preOrder(root->left_child);
Display_preOrder(root->right_child);
}
}
int main() {
struct Node *root = NULL;
root = insert_node(root, 20);
root = insert_node(root, 10);
root = insert_node(root, 60);
root = insert_node(root, 8);
root = insert_node(root, 15);
root = insert_node(root, 42);
root = insert_node(root, 50);
root = insert_node(root, 32);
Display_preOrder(root);
root = delete_node(root, 50);
cout<< "\nAfter deletion: ";
Display_preOrder(root);
return 0;
}
AVL Tree Implementation in Java:
class Node {
int value, height;
Node left_child, right_child;
Node(int data) {
value = data;
height = 1;
}
}
class AVLTree {
Node root;
int height(Node N) {
if (N == null)
return 0;
return N.height;
}
int Max(int num1, int num2) {
return (num1 > num2) ? num1 : num2;
}
Node right_rotate(Node b) {
Node a = b.left_child;
Node t = a.right_child;
a.right_child = b;
b.left_child = t;
b.height = Max(height(y.left_child), height(y.right_child)) + 1;
a.height = Max(height(x.left_child), height(x.right_child)) + 1;
return a;
}
Node left_rotate(Node a) {
Node b = a.right_child;
Node t = y.left_child;
b.left_child = a;
a.right_child = t;
a.height = Max(height(a.left_child), height(a.right_child)) + 1;
b.height = Max(height(b.left_child), height(b.right_child)) + 1;
return b;
}
int get_balance_factor(Node N) {
if (N == null)
return 0;
return height(N.left_child) - height(N.right_child);
}
Node insert_node(Node node, int value) {
if (node == null)
return (new Node(value));
if (value < node.value)
node.left_child = insert_node(node.left_child, value);
else if (value > node.value)
node.right_child = insert_node(node.right_child, value);
else
return node;
node.height = 1 + Max(height(node.left_child), height(node.right_child));
int balance = get_balance_factor(node);
if (balance > 1) {
if (value < node.left_child.value) {
return right_rotate(node);
}
else if (value > node.left_child.value) {
node.left_child = left_rotate(node.left_child);
return right_rotate(node);
}
}
if (balance < -1) {
if (value > node.right_child.value) {
return left_rotate(node);
}
else if (value < node.right_child.value) {
node.right_child = right_rotate(node.right_child);
return left_rotate(node);
}
}
return node;
}
Node min_value(Node node) {
Node current = node;
while (current.left_child != null)
current = current.left_child;
return current;
}
Node delete_node(Node root, int value) {
if (root == null)
return root;
if (value < root.value)
root.left_child = delete_node(root.left_child, value);
else if (value > root.value)
root.right_child = delete_node(root.right_child, value);
else {
if ((root.left_child == null) || (root.right_child == null)) {
Node temp = null;
if (temp == root.left_child)
temp = root.right_child;
else
temp = root.left_child;
if (temp == null) {
temp = root;
root = null;
}
else
root = temp;
}
else {
Node temp = min_value(root.right_child);
root.value = temp.value;
root.right_childt = delete_node(root.right_child, temp.value);
}
}
if (root == null)
return root;
root.height = Max(height(root.left_child), height(root.right_child)) + 1;
int balance = get_balance_factor(root);
if (balance > 1) {
if (get_balance_factor(root.left_child) >= 0) {
return right_rotate(root);
} else {
root.left_child = left_rotate(root.left_child);
return right_rotate(root);
}
}
if (balance < -1) {
if (get_balance_factor(root.right_child) <= 0) {
return left_rotate(root);
} else {
root.right_child = right_rotate(root.right_child);
return left_rotate(root);
}
}
return root;
}
void Display_preOrder(Node node) {
if (node != null) {
System.out.print(node.value + " ");
Display_preOrder(node.left_child);
Display_preOrder(node.right_child);
}
}
private void Display_Tree(Node currPtr, String indent, boolean last) {
if (currPtr != null) {
System.out.print(indent);
if (last) {
System.out.print("R----");
indent += " ";
} else {
System.out.print("L----");
indent += "| ";
}
System.out.println(currPtr.value);
Display_Tree(currPtr.left_child, indent, false);
Display_Tree(currPtr.right_child, indent, true);
}
}
public static void main(String[] args) {
AVLTree tree = new AVLTree();
tree.root = tree.insert_node(tree.root, 20);
tree.root = tree.insert_node(tree.root, 10);
tree.root = tree.insert_node(tree.root, 50);
tree.root = tree.insert_node(tree.root, 8);
tree.root = tree.insert_node(tree.root, 15);
tree.root = tree.insert_node(tree.root, 60);
tree.root = tree.insert_node(tree.root, 42);
tree.root = tree.insert_node(tree.root, 32);
tree.Display_Tree(tree.root, "", true);
tree.root = tree.delete_node(tree.root, 50);
System.out.println("After Deletion: ");
tree.Display_Tree(tree.root, "", true);
}
}
Implementation of AVL Tree in Python:
import sys
class Tree_node(object):
def __init__(self, key):
self.key = key
self.left_child = None
self.right_child = None
self.height = 1
class AVL_Tree(object):
def insert_node(self, root, key):
if not root:
return Tree_node(key)
elif key < root.key:
root.left_child = self.insert_node(root.left_child, key)
else:
root.right_child = self.insert_node(root.right_child, key)
root.height = 1 + max(self.getHeight(root.left_child), self.getHeight(root.right_child))
balanceFactor = self.get_balancing_factor(root)
if balanceFactor > 1:
if key < root.left_child.key:
return self.right_rotate(root)
else:
root.left_child = self.left_rotate(root.left_child)
return self.right_rotate(root)
if balanceFactor < -1:
if key > root.right_child.key:
return self.left_rotate(root)
else:
root.right_child = self.right_rotate(root.right_child)
return self.left_rotate(root)
return root
def delete_node(self, root, key):
if not root:
return root
elif key < root.key:
root.left_child = self.delete_node(root.left_child, key)
elif key > root.key:
root.right_child = self.delete_node(root.right_child, key)
else:
if root.left_child is None:
temp = root.right_child
root = None
return temp
elif root.right_child is None:
temp = root.left_child
root = None
return temp
temp = self.min_value(root.right_child)
root.key = temp.key
root.right_child = self.delete_node(root.right_child, temp.key)
if root is None:
return root
root.height = 1 + Max(self.getHeight(root.left_child), self.getHeight(root.right_child))
balanceFactor = self.get_balancing_factor(root)
if balanceFactor > 1:
if self.get_balancing_factor(root.left_child) >= 0:
return self.right_rotate(root)
else:
root.left_child = self.left_rotate(root.left_child)
return self.right_rotate(root)
if balanceFactor < -1:
if self.get_balancing_factor(root.right_child) <= 0:
return self.left_rotate(root)
else:
root.right_child = self.right_rotate(root.right_child)
return self.left_rotate(root)
return root
def left_rotate(self, z):
y = z.right_child
T2 = y.left_rotate
y.left_child = z
z.right_child = T2
z.height = 1 + max(self.getHeight(z.left_child), self.getHeight(z.right_child))
y.height = 1 + max(self.getHeight(y.left_child), self.getHeight(y.right_child))
return y
def right_rotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left_child), self.getHeight(z.right_child))
y.height = 1 + max(self.getHeight(y.left_child), self.getHeight(y.right_child))
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def get_balancing_factor(self, root):
if not root:
return 0
return self.getHeight(root.left_child) - self.getHeight(root.right_child)
def min_value(self, root):
if root is None or root.left_child is None:
return root
return self.min_value(root.left_child)
def Display_preOrder(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.Display_preOrder(root.left_child)
self.Display_preOrder(root.right_child)
def Display_Tree(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
print(currPtr.key)
self.Display_Tree(currPtr.left_child, indent, False)
self.Display_Tree(currPtr.right_child, indent, True)
myTree = AVL_Tree()
root = None
nums = [20, 10, 50, 8, 15, 42, 60, 32]
for num in nums:
root = myTree.insert_node(root, num)
myTree.Display_Tree(root, "", True)
key = 50
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.Display_Tree(root, "", True)
Complexity Analysis of AVL Tree:
| Scenario/Operation | Insertion | Deletion | Search |
| Average case | O(log n) | O(log n) | O(log n) |
| Best case | O(log n) | O(log n) | O(log n) |
The space complexity of all the operations in an AVL tree is O(n), where n is the number of nodes in the AVL tree.
Applications of AVL Trees:
- Used for performing search operations when the dataset is very large
- Used to index large records in database management systems
Comparison with Red-black Trees:
If we compare AVL trees and red-black trees to a simple binary search tree, then both of them are more efficient than a BST. however, if we compare an AVL tree to a red-black tree, an AVL tree is better in terms of its performance and efficiency. AVL trees are more balanced as compared to red-black trees. But, if there are a lot of insertion and deletion operations, then we prefer red-black trees because AVL trees require a lot of rotations to balance in case of insertion and deletion.
Conclusion:
In this article, we have studied AVL trees, their need and importance, search, insert and delete operations on AVL trees, their implementation in C, C++, Java, Python and applications of AVL trees. From here, we can conclude that AVL trees are one of the most important parts of data structures and they improve the time complexity of trees and have many important applications.