Oftentimes, we have a huge amount of data. It is sometimes difficult to deal with such data especially when it is placed randomly. In such cases, sorting that data becomes of utmost importance. Sorting is required so that searching of data becomes easy.
There are multiple types of sorting algorithms in data structures. Sorting algorithms are broadly classified into two categories:
1. Comparison based
2. Non-comparison based
In comparison-based sorting, we compare the elements, whereas, in non-comparison-based sorting, we don’t compare elements of the list.
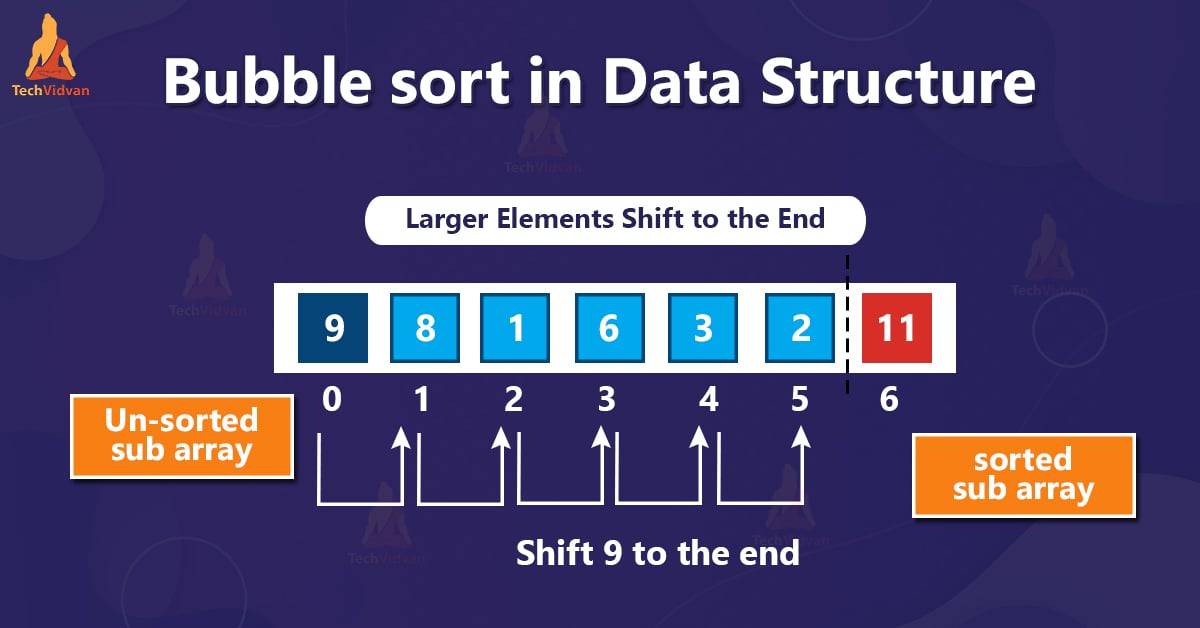
What is Bubble Sort?
Bubble Sort is one of the simplest sorting algorithms. It is also known as Sorting by exchange. It is a comparison-based algorithm. Its time complexity is of the order O(n2) where n is the number of elements.
Working of Bubble Sort
In bubble sort, we compare adjacent elements and whenever we get a pair that is out of order, we swap them.
For n elements, there are n-1 iterations or passes. In every iteration, the largest element reaches its highest iteration.
The steps followed by the bubble sort algorithm are:
1: Start comparing each element with its adjacent element from the starting index.
2: If the current and the next element are out of order, swap them.
3: Repeat step 2 for all the elements of the array/list.
4: Repeat steps 1, 2, and 3 until we have reached the final sorted state of the array.
Bubble Sort Pseudo-code
The pseudo-code for the bubble sort algorithm is:
procedure Bubble_sort(int array)
for(pass=1; pass<=n; pass++)
for(index=0; index <= n-1-pass; index++)
if(array[index] > array[index+1])
swap(array[index], array[index+1])
end if
end for
end for
end procedure
Bubble Sort Example
Let us understand the working of bubble sort with the help of an example.
Suppose we wish to sort the elements of the word “TECHVIDVAN” in alphabetical order.
After the first iteration, the letter ‘V’ will reach the last index.
Iteration 1:
Iteration 2:
Iteration 3:
Iteration 4:
Iteration 5:
Iteration 6:
Iteration 7:
Iteration 8:
Iteration 9:
Finally, after the 9th iteration, we have got our array in ascending order.
Stability of Bubble Sort
A sorting algorithm is said to be stable if it preserves the order of the duplicate elements. In the above example, we have the letter ‘V’ occurring twice. In such cases, the stable algorithms keep the order of appearance of ‘V’ same in both sorted and unsorted arrays.
Bubble sort is also a stable algorithm.
Implementation of Bubble Sort in C
#include <stdio.h>
int main()
{
int Arr[] = {12, 34, 42, 1, 4, 81, 9, 25, 6, 21};
int length = 10;
for (int i = 0; i < length-1; i++)
{
for (int j = 0; j < length-i-1; j++)
{
if (Arr[j] > Arr[j + 1])
{
int temp = Arr[j];
Arr[j] = Arr[j + 1];
Arr[j + 1] = temp;
}
}
}
printf(" Final sorted Array:\n");
for (int i = 0; i < len-1; i++)
{
printf("%d ",Arr[i]);
}
return 0;
}
Implementation of Bubble Sort in C++
#include <bits/stdc++.h>
using namespace std;
void Bubble_sort(int Arr, int n)
{
for (int i = 0; i < n-1; i++)
{
for (int j = 0; j < n-i-1; j++)
{
if (Arr[j] > Arr[j + 1])
{
int temp = Arr[j];
arr[j] = Arr[j + 1];
Arr[j + 1] = temp;
}
}
}
}
int main()
{
int Arr[] = {12, 34, 42, 1, 4, 81, 9, 25, 6, 21};
int len = 10;
Bubble_sort(Arr, len)
cout << "Sorted Array:\n";
for (int i = 0; i < len - 1; i++)
cout << " " << arr[i];
return 0;
}
Bubble Sort Implementation in Java
public class BubbleSort
{
static void Bubble_sort(int Arr[])
{
int i,j,len;
len = arr.length;
Boolean swap;
for (i = 0; i < len-1; i++)
{
for (j = 0; j < len-i-1; j++)
{
if (Arr[j] > Arr[j + 1])
{
int temp = Arr[j];
Arr[j] = Arr[j + 1];
Arr[j + 1] = temp;
}
}
}
System.out.println("Final sorted Array:");
for (i = 0; i < len - 1; i++){
System.out.print(Arr[i]+" ");
}
public static void main(String args[])
{
int[] data = {12, 34, 42, 1, 4, 81, 9, 25, 6, 21};
BubbleSort.Bubble_sort(data);
}
}
Implementation of Bubble Sort in Python
def Bubble_sort(Array):
for i in range(len(Array)):
for j in range(0, len(Array)-i-1):
if Array[j] > Array[j + 1]:
temp = Array[j]
Array[j] = Array[j+1]
Array[j+1] = temp
list = [12, 34, 42, 1, 4, 81, 9, 25, 6, 21]
Bubble_sort(list)
print('Final sorted Array:')
print(list)
Optimized Bubble Sort
In the above example, we can clearly see that the comparisons will be done every time, even if the list is already sorted. This leads to too many extra iterations which are completely unnecessary. These additional iterations increase the execution time of the code.
Thus, we need to modify the bubble sort algorithm. We can optimize this algorithm by using a binary variable ‘flag’ whose initial value is set to False. This binary variable changes its value to true even if one swap occurs in the whole iteration.
At the end of any iteration, if the value of ‘flag’ is still false, it means that the array is now sorted and there is no need for further execution. In this way, it helps in reducing the number of comparisons when the array becomes sorted.
Algorithm for Optimized Bubble Sort
Step 1: For i = 0 to N-1, Repeat:
flag = false
Step 2: For j = i + 1 to N - I,Repeat:
Step 3: If Arr[ j ] > Arr[ i ]
swap Arr[ j ] and Arr[ i ]
flag = true
Step 4: If flag == false
Goto step 5
Step 5: stop
Pseudo-code for Optimized Bubble Sort
procedure Bubble_sort(int Array)
len = Array.length;
for i = 0 to loop-1 do:
flag = false
for j = 0 to loop-1 do:
if Array[j] > Array[j+1] then
swap( list[j], list[j+1] )
flag = true
end if
end for
If flag == false
break;
end for
return Array
end procedure
Optimized Bubble Sort Implementation in C
#include <stdio.h>
void main()
{
int Arr[] = {12, 34, 42, 1, 4, 81, 9, 25, 6, 21};
int len = 10, flag;
for (int i = 0; i < len-1; i++)
{
flag=0;
for (int j = 0; j < len-i-1; j++)
{
if (Arr[j] > Arr[j + 1])
{
int temp = Arr[j];
Arr[j] = Arr[j + 1];
Arr[j + 1] = temp;
flag =1;
}
}
if (flag == 0)
break;
}
printf("Final sorted Array:\n");
for (int i = 0; i < len - 1; i++)
{
printf("%d ",Arr[i]);
}
}
Implementation of Optimized Bubble Sort in C++
#include <iostream>
using namespace std;
int main()
{
int arr[] = {12, 34, 42, 1, 4, 81, 9, 25, 6, 21};
int len = 10;
int flag;
for (int i = 0; i < len-1; i++)
{
flag=0;
for (int j = 0; j < len - i - 1; j++)
{
if (Arr[j] > Arr[j + 1])
{
int temp = Arr[j];
Arr[j] = Arr[j + 1];
Arr[j + 1] = temp;
flag =1;
}
}
if (flag == 0)
break;
}
cout << "Final sSorted Array:\n";
for (int i = 0; i < len - 1; i++)
{
cout << " " << Arr[i];
}
}
Optimized Bubble Sort Implementation in Java:
public class BubbleSort
{
static void Bubble_sort(int Arr[])
{
int i,j,len;
len = arr.length;
Boolean flag;
for (i = 0; i < len-1; i++)
{
flag = false;
for (j = 0; j < len-i-1; j++)
{
if (Arr[j] > Arr[j + 1])
{
int temp = Arr[j];
Arr[j] = Arr[j + 1];
Arr[j + 1] = temp;
flag = true;
}
}
if (flag == false)
break;
}
System.out.println("Final sorted Array:");
for (i = 0; i < len - 1; i++)
System.out.print(Arr[i]+" ");
}
public static void main(String args[])
{
int[] data = {12, 34, 42, 1, 4, 81, 9, 25, 6, 21};
BubbleSort.Bubble_sort(data);
}
}
}
Optimized Bubble Sort Implementation in Python
def Bubble_sort(Array):
for i in range(len(Array)):
flag = false
for j in range(0, len(Array) - i - 1):
if Array[j] > Array[j + 1]:
temp = Array[j]
Array[j] = Array[j+1]
Array[j+1] = temp
flag = true;
if flag == false:
break;
list = [12, 34, 42, 1, 4, 81, 9, 25, 6, 21]
Bubble_sort(list)
print('Sorted Array:')
print(list)
Complexity of Bubble Sort
Time complexity:
Time complexity in bubble sort is mainly due to two operations:
1. Comparisons
2. Swaps
In bubble sort, we compare adjacent elements. Thus, the number of comparisons will be:
| Iteration | Number of comparisons |
| 1 | (n-1) |
| 2 | (n-2) |
| 3 | (n-3) |
| . | . |
| . | . |
| . | . |
| n-2 | 2 |
| n-1 | 1 |
Thus, the total number of comparisons are:
(n-1) + (n-2) + (n-3) + ………… + 2 + 1 = n(n-1)/2
= O(n2)
- In the best case, the array is already sorted. Thus, there will be zero swaps.
- In the average case, the array is jumbled. The number of swaps will be of O(n2).
- In the worst case, the number of swaps will be equal to the number of comparisons i.e. O(n2).
| Scenario | Time complexity |
| Best case | O(1) |
| Average case | O(n2) |
| Worst case | O(n2) |
Space complexity of Bubble Sort
Only one extra variable ‘temp’ is used. Thus the space complexity will be of O(1).
Advantages of Bubble Sort
- Easy to implement and understand.
- Stable sorting algorithm.
- Useful in computer graphics to resolve very small errors.
- Its space complexity is very less in comparison to other sorting algorithms.
Disadvantages of Bubble Sort:
- It is the high time complexity of O(n2) and therefore higher execution time.
- It is not preferable for a large amount of data.
Conclusion
The bubble sort algorithm is the easiest out of all sorting algorithms in terms of implementation. However, it takes a lot of time for execution when the amount of data is large. Thus, when the data set is small, bubble sort is one of the best algorithms to apply.