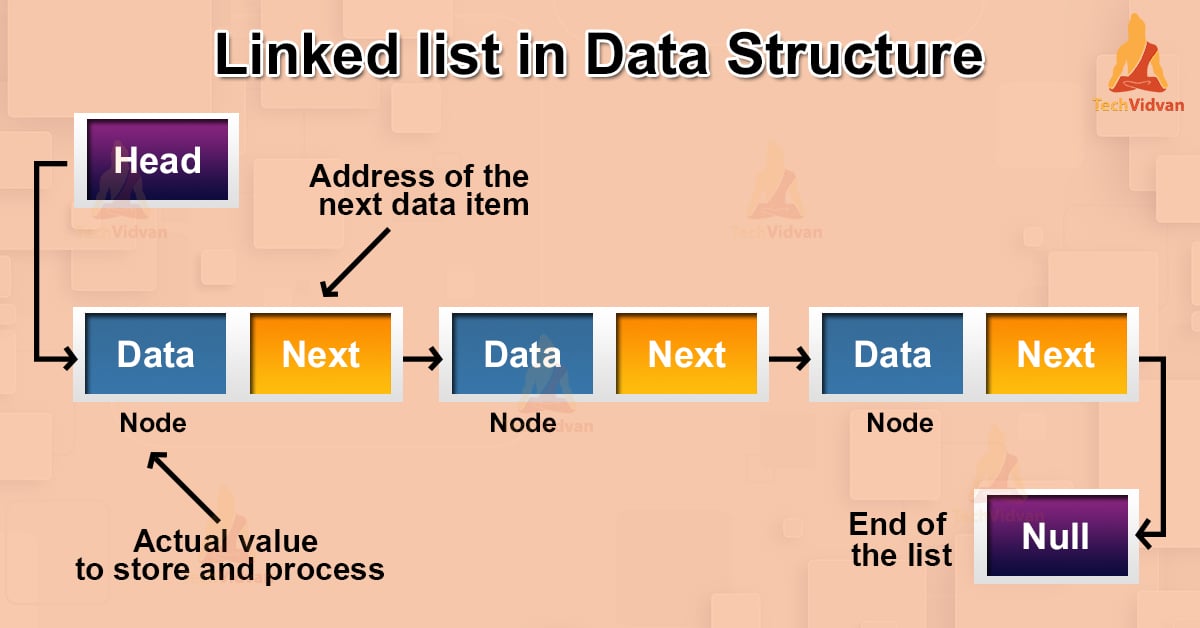
There are broadly two types of Data structures: Linear and Non-linear. Linear data structures are those in which every element is connected to the previous element and the elements are present at a single level.
Some examples of linear data structures are- Arrays, linked lists, stack,s and queues. Thus, a linked list is a linear data structure in which elements are not stored contiguously in the memory.
Let’s learn about Linked List in Data Structure.
What is a Linked list?
1. A linked list a collection of randomly stored elements in the memory. These elements are called nodes.
2. We use pointers to connect and maintain the linear order between these random data points.
3. Every node of a linked list consists of at least two parts-
- Data
- Address of next node(pointers)
The above diagram shows that in a linked list, the elements are not stored contiguously but it appears that they are stored contiguously.
The most important thing in a linked list is the pointer. We need to have a starting pointer (HEAD) to access the linked list. The last node in the linked list has a pointer to NULL.
Properties of linked list in Data Structure
1. The elements of the linked list may or may not be present contiguously in the memory.
2. We need not declare the list size in advance.
3. We can allocate the memory dynamically whenever we need to add more nodes or perform any other operation on the list.
4. The linked list cannot contain an empty node.
5. A node in a linked list is a combination of two data types- a pointer and a primitive data type such as int or float. Therefore, we use structures to implement a linked list.
Applications of Linked List in Data Structure
1. We can implement stack and queue data structures using a linked list.
2. It is used in the implementation of graphs. Example- Adjacency list representation in a graph makes use of a linked list.
3. Symbol table management in compiler design uses a linked list.
4. It is used to prevent collision in hashing.
5. Linked list is used for DMA (Dynamic Memory Allocation).
6. We can use linked lists for performing arithmetic operations on long int.
7. Representation of a sparse tree matrix also requires a linked list.
Data Structure Linked List vs Array
Both arrays and linked lists have their own use cases, advantages as well as disadvantages.
Let us see a few comparisons between them.
| ARRAY | LINKED LIST |
| Arrays are contiguously stored in the memory. | Linked lists are not necessarily contiguous inside the memory. |
| The array size should be declared inside the program in advance. | We need not declare the size of the list in advance. |
| It is difficult to change the size of the array afterwards. | We can expand or shrink a linked list any time during the execution of the program. |
| Arrays allow random access of elements. | In a linked list, we cannot randomly access any element, we need to traverse the list from the beginning. |
| Arrays have slower insertion or deletion time as compared to linked lists. | Linked lists have a slower search time because of the absence of random access. |
| Arrays require less memory per element. | Lists require more memory because we need to maintain extra pointers. |
Types of linked lists
There are three types of lists in data structures:
1. Singly-linked list
2. Doubly linked list
3. Circular linked list
In this article, we are going to study about singly list.
Basic Operations on Linked List
There are certain basic operations that a linked list data structure supports. These operations are:
1. Traversal:
It means visiting each node from the beginning till the end.
2. Insertion:
This operation inserts an element at any given position in the list.
3. Deletion:
Deletion operation helps in deleting a node from the linked list.
4. Display:
This operation is used to print/display all the data elements of the linked list.
5. Search:
search operation helps in searching an element by traversing it.
Declaration and Initialization of a Node in a linked list:
A node is a heterogeneous data type. Therefore, we use a structure to create it.
struct Node
{
int data; //the first part of the node where data is stored
struct node *Next; //Self-referencing structure. It links two nodes.
};
The linked list supports dynamic memory allocation. Therefore, we will use the functions malloc, calloc and realloc for memory allocation.
The code will be:
struct Node *Head, *Ptr; //Declaring two pointers- Head and Ptr Ptr = (struct Node *)malloc(sizeof(struct Node *)); //Initializing Ptr
Dynamic memory is allocated inside the heap, which is why we need functions like malloc. Here, malloc will return the address of the node.
Traversal in a Singly Linked List
Traversal means visiting each node of the linked list. Once the node has been created, we can do its traversal in the following way.
struct Node *Ptr;
Ptr = Head;
while(Ptr != NULL)
{
Print (Ptr→data);
Ptr = Ptr→Next;
}
The time complexity for the above pseudo-code will be O(n).
Insertion in a Linked List
When we talk about insertion in a linked list, we take into consideration three different cases:
1. Insertion at the beginning of the list
2. Insertion after a particular node.
3. Insertion at the end of the list
1. Insertion at the beginning:
Insertion at the beginning means we will insert a node at the front of the list in the following way:
The above diagram shows that we have a linked list of the following elements: 10→20→30.
Once we insert a new node at the beginning, the list will be 50→10→20→30.
Pseudo-code:
Void Insert_at_beginning(int key)
{
struct Node *temp; //temp is a pointer pointing to the node to be inserted.
temp = (struct Node*) malloc(sizeof(struct Node));
if(temp != NULL)
{
temp→data = key; //key is the data value to be inserted
temp→next = Head; //this step will make the incoming node the first node.
}
}
2. Insertion after a particular node:
We need to traverse all the nodes before the position of insertion of the new node. For doing this, we maintain an additional temporary pointer.
For example, suppose we wish to link all the letters of the word ‘TECHVIDVAN’ and we forgot to add “H”.
We can insert this ‘H’ once the list is created as shown below.
In this case, we will have a temporary pointer named ‘temp’. This pointer temp will be pointing to ‘C’ because we need to insert ‘H’ after ‘C’.
The lines of code that will help to do this will be:
temp->Next = Ptr->Next; Ptr->Next = temp;
3. Insertion at the End:
To insert a node at the end of the list, we first need to traverse the whole list.
The function for insertion at the end is:
void Insert_at_end(int key)
{
struct Node *temp, *Ptr;
temp = (struct Node*) malloc(sizeof(struct Node));
if(temp != NULL)
{
temp->data = key;
temp->Next = NULL;
if(Head == NULL) //This will be true if the list is initially empty
{
Head = temp;
return;
}
Ptr = Head;
while(Ptr->Next != NULL)
Ptr->Next = temp;
}
}
Time complexity of Insertion in Linked List
| Insertion operation | Complexity |
| At the beginning | O(1) |
| After a particular node | O(1) |
| At the end | O(n) |
Deletion from a Linked List:
Just like insertion, deletion also works in three different cases:
1. Deletion from beginning
2. Deletion at the end
3. Deleting a node other than the first and the last node
1. Deletion from the beginning:
It involves deleting the first node of the linked list.
Suppose we initially had the linked list elements as 10→20→30→40.
If we perform deletion of one node at the beginning, the linked list will be:
20→30→40.
The function for performing deletion at the beginning is:
void Delete_from_beginning(int key)
{
struct Node *Ptr = Head;
if(Head == NULL) //i.e. If the list is empty
{
return;
}
Head = Head->Next; //linking Head with the 2nd node of the list
free(Ptr);
}
Whenever we delete a node, we make the memory area occupied by that node free by using the ‘free’ function. Otherwise, it might lead to a memory leakage problem.
2. Deletion at the end:
For deletion of the last node, we need to make the address of the second last node point to NULL. For doing this, we will make use of an extra pointer named ‘Prev’.
While deleting the last node, we will first free the last node and then make the Next of the second last node as NULL.
The function for deletion at the end will as follows:
void Delete_at_end(int key)
{
struct Node *Ptr = Head;
struct Node *Prev = NULL;
if(Head == NULL) //If the list is empty
{
return;
}
if(Head->Next == NULL) //If the list has only one element
{
Head = NULL;
free(Ptr);
}
else
{
while(Ptr->Next != NULL)
{
Prev = Ptr;
Ptr = Ptr->Next;
}
free(Ptr);
}
}
3. Deletion after a particular node:
If we have the address of a particular node, we can always delete the node next to it.
Let us consider a linked list: 10→20→30→40.
Suppose we wish to delete 20 from it, we will delete the node containing 30 and then rewrite the value of 20 as 30.
The lines of code for doing this will be:
Ptr->data = Ptr->Next->data; Ptr = Ptr->Next; Ptr->Next = Ptr->Next->Next; free(Ptr);
Thus, after deleting 20, the new list will be 10→30→40.
Time complexity for Deletion operation:
| Deletion operation | Complexity |
| At the beginning | O(1) |
| After a particular node | O(1) |
| At the end | O(n) |
Reversing a linked list:
To reverse a linked list, we need to reverse the pointers.
For example, if the list is 10→20→30→40,
On reversing we will have 10←20←30←40 and 10 will point to NULL.
The recursive approach to reverse a list is as follows:
int Reverse_list(struct Node *Head)
{
struct Node *remaining;
if (Head == NULL || Head->Next == NULL)
return Head;
Node* remaining = Reverse_list(Head->Next);
Head->Next->Next = Head;
Head->Next = NULL;
return remaining;
}
Uses of Linked List
1. The size of the linked list is limited to the memory size due to dynamic memory allocation. That is why, we need not declare the size of the list beforehand, rather we can do that at run time.
2. A linked list can never contain an empty node.
3. Although a linked list is a linear data structure, it is unnecessary to store it contiguously in the memory. This is because the list is connected through addresses/pointers. This helps in the efficient utilization of memory space.
4. The singly linked list can store the values of primitive data types such as int, char, float. The list can also store objects when working in OOP.
Conclusion
A singly linked list of a lot of use in Computer science. Its main application lies in the implementation of other data structures. Therefore, it is very important to have a good understanding of this data structure.
In this article, we studied a singly linked list. In the upcoming articles, we will read about the other remaining types of lists.