Binary Tree in C – Types and Implementation
C programming language provides awesome and useful features and functionalities to the programmers. In C, you can make use of some data structures which will help you in better and efficient coding. So, in this tutorial, we are going to discuss Binary Tree in C. It is one of the popular concepts of the C programming language. But firstly we will learn about Tree in C.
What are Trees in C?
As you know that arrays, linked lists, Stacks and Queues are linear data structures. And on the other hand, Trees are hierarchical data structures. A tree includes multiple nodes. In C, we call it a Binary Tree. A tree is referred to as a finite and non-empty set of elements in mathematical terminology.
Tree Terminologies:-
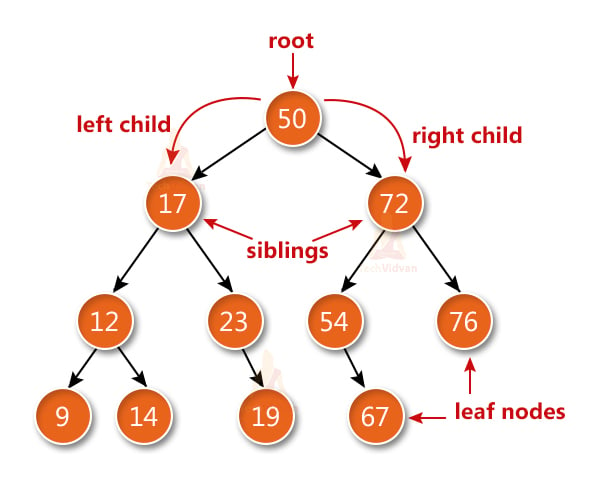
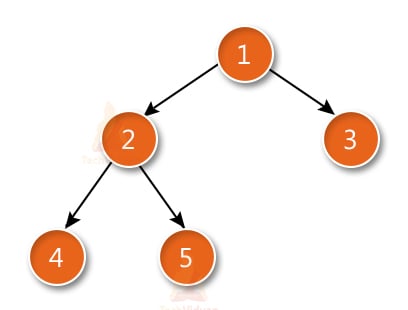
1. Root:- A root is a node without a parent. In the above image, 50 is the root node.
2. Siblings:- Siblings mean that nodes which have the same parent node. In the above image, 17 and 72 are siblings because they have 50 in common.
3. Internal Node:- Internal Node means that a node which has at least a single child. In the above image, 17, 72, 12, 23, 54 are internal nodes.
4. External Node:- External Node means that a node which has no children. It is also known as leaf. In the above image, 67 and 76 are external nodes.
5. Ancestors:- Ancestors include the parent, grandparent and so on of a node. In the above image, the ancestors of 23 are 17 and 50.
6. Descendants:- Descendants are the opposite of ancestors, It includes the child, grandchild and so on of a node. In the above image, the descendants of 17 are 12,23,19,9,14 and 50.
7. Edge:- An edge means a connection between one node to another node.
8. Path:- Path is a combination of nodes and edges connected with each other. In the above image, 50 to 19 is a path.
9. Depth:- You can calculate depth by the number of edges from node to the root of the tree.
10. Height:- Height is the maximum depth of a node.
11. Level:- Level of a node is equal to depth of the node+1.
Applications of trees:-
Following are some of the main applications of trees.
- Used to manipulate hierarchical data or information.
- Through trees, Searching is very easy.
- Router Algorithms.
- Used to manipulate sorted lists of data.
- With this, you can form multi stage decision making.
Binary Tree in C:-
A tree is called binary when its elements have at most two children. In a binary tree, each element should have only 2 children and these are known as left and right.
Representation of Binary Tree in C:-
The value of root is NULL when a tree is empty. It works on O(logN) for insert, search and delete operations.
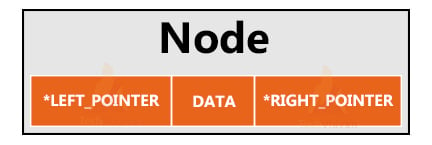
A tree node includes the following parts:-
- Data
- Pointer to the left child
- Pointer to the right child
Using structures in C, you can represent a tree node.
Example:- A tree node with integer data
struct node
{
int data;
struct node *left_child;
struct node *right_child;
};
In the above example, the *left_child is the pointer to the left child which can or cannot be NULL and the *right_child is the pointer to the right child which can or cannot be NULL.
Need for binary trees:-
In C, Binary trees have some exciting and useful applications which you can implement.
- With the help of a binary search tree, you can easily find an element in a huge set because it is fast and efficient.
- Using binary trees, you can implement heapsort.
- To store information in databases, your best way is to make use of binary trees.
Types of Binary Tree in C:-
In C, there are two types of binary tree such as:-
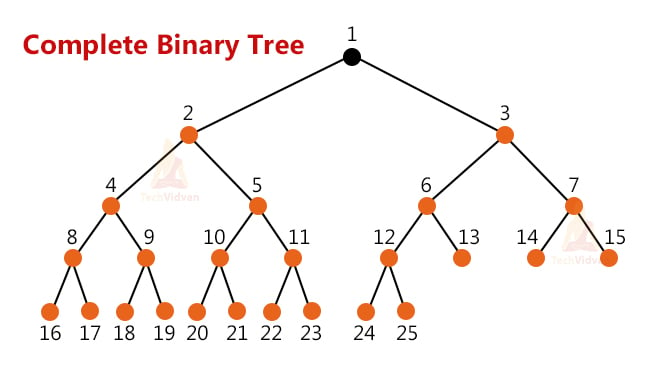
1. Complete Binary Tree:-
A binary tree is complete when all nodes are as far left as possible and every level except the last level is filled completely.
2. Full Binary Tree:-
A binary tree is called Full binary tree when each node of the tree has two children except the leafs(external nodes).
Implementation of Binary Tree in C:-
Similarly like Linked Lists, you can implement a binary tree in C. We use structures to implement a binary tree in C.
1. Declaration of a binary tree:-
First, you have to declare it before implementing it. Following is the code to declare a binary tree:-
struct node
{
int data;
struct node *left_child;
struct node *right_child;
};
2. Creating Nodes in a binary tree:-
It is like creating data elements in linked lists. A binary tree is created by inserting the root node and its child nodes. Following is the code to create nodes in a binary tree:-
void insert(node ** binary_tree, int value) {
node *tmp = NULL;
if(!(*binary_tree)) {
tmp = (node *)malloc(sizeof(node));
tmp->left = tmp->right = NULL;
tmp->data = value;
*binary_tree = tmp;
return;
}
if(value < (*binary_tree)->data) {
insert(&(*binary_tree)->left, value);
} else if(value > (*binary_tree)->data) {
insert(&(*binary_tree)->right, value);
}
}
3. Searching into a binary tree:-
In the binary tree, you can search for the values of the nodes. Below is the code to perform a search operation on a binary tree.
node *search(node ** binary_tree, int value) {
if(!(*binary_tree)) {
return NULL;
}
if(value == (*binary_tree)->data) {
return *binary_tree;
} else if(value < (*binary_tree)->data) {
search(&((*binary_tree)->left), value);
} else if(value > (*binary_tree)->data){
search(&((*binary_tree)->right), value);
}
}
The above code will search for the value of a node whether the node of the same value exists or not.
4. Deletion of a binary tree:-
You can delete a binary tree by removing the child nodes and the root node. Below is the code snippet to delete a binary tree.
void delete_tree(node * binary_tree) {
if (binary_tree) {
delete_tree(binary_tree->left);
delete_tree(binary_tree->right);
free(binary_tree);
}
}
5. Displaying the binary tree:-
You can display a binary tree in three forms such as:-
- Pre-Order:- It displays in order. First root node, then left node and then right node.
- In-Order:- It displays first left node, then root node and then right node.
- Post-Order:- It displays first left node, then right node and then root node.
void display_preorder(node * binary_tree) {
if (binary_tree) {
printf("%d\n",binary_tree->data);
display_preorder(binary_tree->left);
display_preorder(binary_tree->right);
}
}
void display_inorder(node * binary_tree) {
if (binary_tree) {
display_inorder(binary_tree->left);
printf("%d\n",binary_tree->data);
display_inorder(binary_tree->right);
}
}
void display_postorder(node * binary_tree) {
if (binary_tree) {
display_postorder(binary_tree->left);
display_postorder(binary_tree->right);
printf("%d\n",binary_tree->data);
}
}
Example:- Implementation of Binary Tree in C
#include<stdio.h>
#include<stdlib.h>
struct node
{
int value;
struct node *left_child, *right_child;
};
struct node *new_node(int value)
{
struct node *tmp = (struct node *)malloc(sizeof(struct node));
tmp->value = value;
tmp->left_child = tmp->right_child = NULL;
return tmp;
}
void print(struct node *root_node) // displaying the nodes!
{
if (root_node != NULL)
{
print(root_node->left_child);
printf("%d \n", root_node->value);
print(root_node->right_child);
}
}
struct node* insert_node(struct node* node, int value) // inserting nodes!
{
if (node == NULL) return new_node(value);
if (value < node->value)
{
node->left_child = insert_node(node->left_child, value);
}
else if (value > node->value)
{
node->right_child = insert_node(node->right_child, value);
}
return node;
}
int main()
{
printf("TechVidvan Tutorial: Implementation of a Binary Tree in C!\n\n");
struct node *root_node = NULL;
root_node = insert_node(root_node, 10);
insert_node(root_node, 10);
insert_node(root_node, 30);
insert_node(root_node, 25);
insert_node(root_node, 36);
insert_node(root_node, 56);
insert_node(root_node, 78);
print(root_node);
return 0;
}
Output:-
TechVidvan Tutorial: Implementation of a Binary Tree in C!
10
25
30
36
56
78
Summary
In this tutorial, we learnt about Binary trees in C. We discussed what are trees and what are binary trees. We also discussed the terminologies of a tree and types of binary trees in C. Then we discussed the need for binary trees. We also talked about how we can implement a binary tree in C. And we performed some basic operations on a binary tree such as insertion, deletion, searching and displaying.