Public Key Cryptography in Blockchain
Public-key cryptography, also called asymmetric cryptography, is basically a cryptographic system that uses a public key and a private key. Both the keys are non-identical and generated using cryptographic algorithms based on complex mathematics. They are designed in such a way that the public key can be openly distributed whilst the private key has to remain private.
The public key is used to encrypt a message which can be decrypted only by the private key. This method is popularly employed in computers to increase data security while online transfer to prevent thefts or tampering.
The keys are computed such that it is impossible to find the private key even if the public key is known. Thus, private keys can be shared freely, allowing easy encryption of data. However, private keys have to be kept a secret so that only concerned individuals or entities can decrypt it or create digital signatures
Public key cryptography allows a sender to combine their message with a private key in order to create a short digital signature on the message. This digital message can be used to verify the authenticity of the message by anyone who has access to the public key. It is proof that the sender actually has the private key needed to decrypt the message and that it has not been altered.
Storing the keys
Since public keys are free to be shared, but are too long to be remembered, they are stored on digital certificates, which aid in their secure sharing. However, private keys have to be guarded and can be stored in the operating system or preferably on hardware containing drives.
RSA Cryptosystem
The most popularly used public key cryptosystem (Cryptographic System) is RSA (Rivest-Shamir-Adleman). The backbone of this system iis that it is difficult to factorise a large integer.
In the RSA cryptosystem, the public key consists of two numbers, and one of those is the product of two large prime numbers. The private key is also derived from the same two prime numbers. Hence, if someone can factorize that large number, the private key will be compromised. Thus, the strength of encryption is entirely dependent on the key size, and increasing the key size by 2 or 3 times can increase the encryption strength exponentially.
Usually, RSA keys are 1024 or 2048 bits long, but with cybercrime at an all time high, it is widely believed that the 1024 bit keys could be broken in the near future. However, today it is nearly impossible.
RSA Analysis
The security of RSA depends on the strengths of the following 2 functions :
1. Encryption Function: It is a one-way function to convert plaintext to ciphertext and cannot be reversed without the private key.
2. Key Generation: The RSA private key cannot be generated from the public key unless an attacker can find the product of the two prime numbers used to make the keys.
If at any time in the future, a sophisticated technique to predict the encryption function from the public key to figure out the private key is generated, the RSA will become obsolete as it will not be able to provide data security at all.
Generation of RSA Key Pair
To participate in communication using encryption, a person or party must generate a pair of keys, namely a public key and a private key. The steps for generating keys are outlined below −
1. Create the RSA modulus (n)
- Select two large primes, p and q.
- Calculate n=p*q.
2. Find Derived Number (e)
- Number e must be greater than 1 and less than (p − 1)(q − 1).
- e and (p − 1)(q − 1) must be coprime.
- The numbers n and e form the RSA public key.
3. Generate the private key
- Private Key d is calculated from p, q, and e. For defined n and e, there exists a unique number d.
- Number d is the number less than (p – 1)(q – 1) such that when multiplied by e, it is equal to 1 modulo (p – 1)(q – 1).
- This relationship is written mathematically as ed = 1 mod (p − 1)(q − 1)
The Extended Euclidean Algorithm takes p, q, and e as input and gives d as output.
Example of generating RSA Key Pair
Let’s understand using an example. Here, we have taken smaller values of p and q for easier calculations. However, the values of p and q to make a real RSA key are much higher.
- Let two primes be p = 7 and q = 13. Thus, modulus n = pq = 7 x 13 = 91.
- Select e = 5, which is a valid choice since there is no number that is common factor of 5 and (p − 1)(q − 1) = 6 × 12 = 72, except for 1.
- The pair of numbers (n, e) = (91, 5) forms the public key and can be made available to anyone whom we wish to be able to send us encrypted messages.
- Input p = 7, q = 13, and e = 5 to the Extended Euclidean Algorithm. The output will be d = 29.
- Check that the d calculated is correct by computing −
de = 29 × 5 = 145 = 1 mod 72
Hence, the public key is (91, 5) and the private key is (91, 29).
Encryption and Decryption
RSA Encryption
- Suppose you wish to send some text message to someone with a public key(n, e).
- You will represent the plaintext as a series of numbers less than n.
- To encrypt the first plaintext P, which is a number modulo n. The encryption process is a simple mathematical step as C = P^e mod n
- Here, the ciphertext C equals the plaintext P multiplied by itself e times and then reduced modulo n. Thus, C is also a number less than n.
- Returning to our Key Generation example with plaintext P = 10, we get ciphertext C = 10^5 mod 91
RSA Decryption
- Assume that the receiver of the public-key pair (n, e) has received a ciphertext C.
- Receiver raises C to the power of his private key d. The result modulo n will be the plaintext P = C^d mod n
- Returning again to our numerical example, the ciphertext C = 82 would get decrypted to number 10 using private key 29 as Plaintext = 82^29 mod 91 = 10
RSA Analysis
RSA Cryptosystem is currently the most popular public-key cryptosystems and its strength and security is based on two things:
- Encryption Function − It is a one way function to convert plaintext into ciphertext and cannot be reversed with knowing the private key d.
- Key Generation − The private key cannot be deduced from the public key without factoring the modulus n. Since it is almost impossible to do that, this is also a one-way function that ensures safety of the RSA System.
If anytime in the future either of two functions stop being one-way, then RSA will be broken.
ElGamal Cryptosystem
There are a number of public-key cryptosystems that have been proposed overtime. One such is ElGamal, called the Elliptical Curve Variant, based on the Discrete Logarithm Problem. Let us try to understand this system.
Generation of ElGamal Key Pair
Each user of ElGamal cryptosystem generates the key pair by−
1. Choosing a large prime p.
2. Choosing a generator element g.
- This number must be between 1 and (p − 1), but cannot be any number.
- It is a generator of the multiplicative group of integers modulo p. This means for every integer m co-prime to p, there is an integer k such that g^k=a mod n. For example, 3 is generator of group 5 (Z5 = {1, 2, 3, 4}).
| N | 3n | 3n mod 5 |
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
- Choosing the private key – The private key x is any number bigger than 1 and smaller than p−1.
- Computing part of the public key – The value y is computed from the parameters p, g and the private key x as y = g^x mod p
- Obtaining Public key – The ElGamal public key consists of the three parameters (p, g, y).
For example, suppose that p = 17 and that g = 6 (It can be confirmed that 6 is a generator of group Z17). The private key x can be any number bigger than 1 and smaller than 71, so we choose x = 5. The value y is then computed as y = 6^5 mod 17 = 7
Thus the private key is 62 and the public key is (17, 6, 7).
Encryption and Decryption
ElGamal Encryption
Suppose you wish to send a plaintext to someone whose ElGamal public key is (p, g, y), then −
1. Sender represents the plaintext as a series of numbers modulo p.
2. To encrypt the first plaintext P, which is represented as a number modulo p. The encryption process to obtain the ciphertext C is as follows −
- Randomly generate a number k;
- Compute two values C1 and C2, where −
C1 = g^k mod p
C2 = (P*y^k) mod p
3. Send the ciphertext C, consisting of the two separate values (C1, C2), sent together.
4. Referring to our ElGamal key generation example given above, the plaintext P = 13 is encrypted as follows −
- Randomly generate a number, say k = 10
- Compute the two values C1 and C2, where −
C1 = 6^10 mod 17
C2 = (13*7^10) mod 17 = 9
5. Send the ciphertext C = (C1, C2) = (15, 9).
ElGamal Decryption
1. To decrypt the ciphertext (C1, C2) using private key x, the following two steps are taken −
- Compute the modular inverse of (C1)^x modulo p, which is (C1)^-x , generally referred to as the decryption factor.
- Obtain the plaintext by using the following formula −
C2 × (C1)^-x mod p = Plaintext
2. In our example, to decrypt the ciphertext C = (C1, C2) = (15, 9) using private key x = 5, the decryption factor is
15-5 mod 17 = 9
3. Extract plaintext P = (9 × 9) mod 17 = 13.
ElGamal Analysis
In the ElGamal system, each user has a private key x. and has three components of public key − prime modulus p, generator g, and public Y = g^x mod p. The strength of the ElGamal is based on the difficulty of the discrete logarithm problem.
The secure key size is generally > 1024 bits. Today even 2048 bits long keys are used. On the processing speed front, Elgamal is quite slow; it is used mainly for key authentication protocols. Due to higher processing efficiency, Elliptic Curve variants of ElGamal are becoming increasingly popular.
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) describes a suite of cryptographic tools and protocols which relies on special versions of the discrete logarithm problem for its security. It does not use numbers modulo p. ElGamal encryption and Digital Signature Algorithm are two of the cryptographic schemes included in ECC.
We can obtain an equivalent level of security by using an elliptic curve instead of p-values modulo p. Furthermore, shorter keys can be used to obtain an equivalent level of security if we use elliptic curve-based variants.
The shorter keys result in two benefits −
- Ease of key management
- Efficient computation
Difference between Encryption and Public key Encryption in blockchain
1. Work-related
While normal encryption algorithms employ one key for encryption as well as decryption, public key encryption uses a pair of keys, one for encryption and the other for decryption. Hence, both processes follow different algorithms.
2. Security
All conventional encryption methods are reliant on the secrecy of the key. As long as the key is secret it is quite impossible to decrypt the message. But for public key encryption only one of the two keys has to be kept a secret. If one key is made public, it will have absolutely no harm in the security of the data.
Example:
Imagine that you want to send an encrypted message to your friend, Ram using public key encryption. Public key of Ram is available in the Public key register, you can use this key to write your encrypted message and send it to Ram. However, since no one else but Ram has access to the private key needed to decrypt this message, no one else will be able to decode your message. As soon as Ram receives your message, he will use his private key to decrypt it!
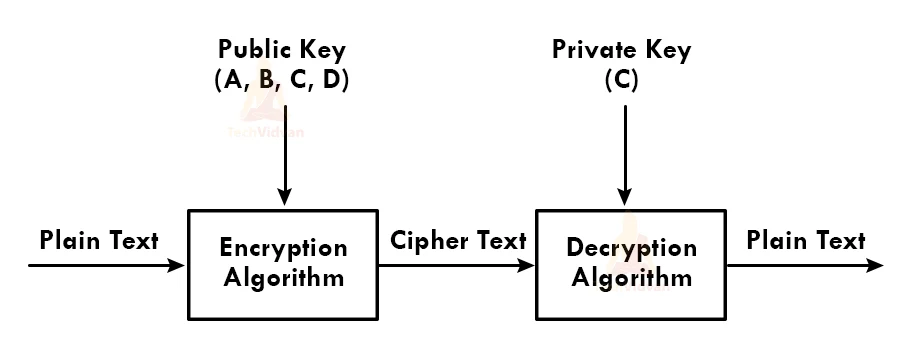
Components of Public Key Encryption
1. Plain Text: Plain text refers to the original message the sender intends to pass to the receiver in a readable format.
2. Ciphertext: This refers to the plain text after it has been encrypted by the encryption algorithm. The cipher text cannot be understood without decryption.
3. Encryption algorithm: This refers to the algorithm used to convert plain text to cipher.
4. Decryption Algorithm: This refers to the set of instructions to be followed in order to convert the cipher text back to plain text in a readable format.
5. Public and private key: The public key encryption algorithm uses a public key to encrypt the data and a private key to decrypt it.
Characteristics of Public Key Encryption
Let’s have a look at some of the important properties of Public Key Encryption :
1. A pair of unsymmetric keys, namely public and private key used for encryption and decryption respectively.
2. All receivers have their own private keys
3. Complex encryption algorithms prevent attackers from trying to hack the encryption key.
4. Digital signatures allow an extra layer of authentication to prove data integrity.
5. Public (or encryption) keys can be shared widely, thereby allowing easy data encryption.
Weaknesses of public-key encryption
1. If by any chance the private key is lost, the data is also lost forever and cannot be decrypted.
2. Public key encryption is susceptible to brute force attacks.
3. Attackers can try to disrupt the public key communication and even modify the public keys.
Applications of public key cryptography
1. Encryption/Decryption: The primary application of public key cryptography is to send and receive encrypted messages securely.
2. Digital signature: Sending plain text in an encrypted format using one’s own private key can be used as a form of authentication. This is because the receiver can decrypt the cipher text using the sender’s public key and hence, verify that the sender is legit. Thus, acting like a digital signature.
3. Key exchange: Both Key-management and secure data transmission can be achieved using this algorithm.
