Binary Search in Data Structure
There are various ways to search a particular element from a given list. One of them is Binary search.
When there exists so much data everywhere, it is very necessary to have a good searching method to search for the particular data in lesser time.
Binary search works faster than linear search. It is one of the fastest searching algorithms.
What is Binary Search?
It is a searching technique. It is based upon Divide and conquer strategy. Binary search is applicable only on sorted data. It takes O(log n) time for completion.
It divides the given array into halves and then checks the middle element. If the middle element is smaller than the element to be searched, the algorithm selects the second half of the array and discards the first half.
Thus, at every step, the binary search algorithm keeps on discarding half of the array based on the value of the middle element. This process continues until the array becomes of the size 1 or 2 and the algorithm finally gets the required element.
If the search is successful i.e. the element is present in the array, it returns the index of that element. If the element is not present inside the array, the algorithm returns -1.
Working of Binary Search
Let us understand the working of a binary search algorithm with the help of an example.
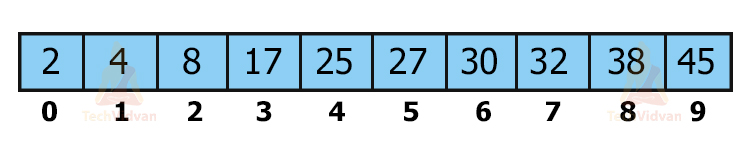
Consider a sorted array having 10 elements as shown:
Suppose we wish to search 38 in the array.
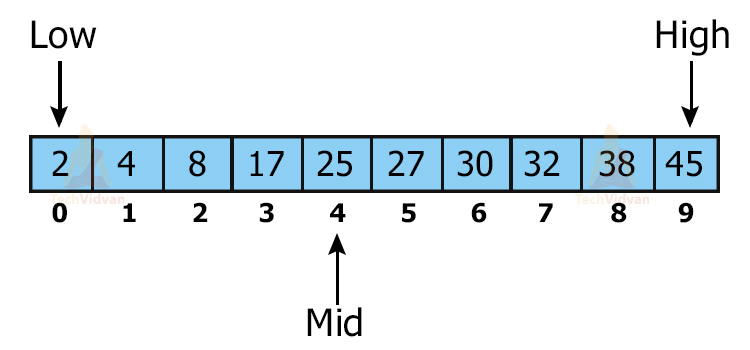
Step 1: Find the middle element of the array.
index(Middle) = index(low) + index(high – low)/2.
Here, middle = 0 + (9-0)/2 = 4 i.e. the element at the 4th index i.e. 25.
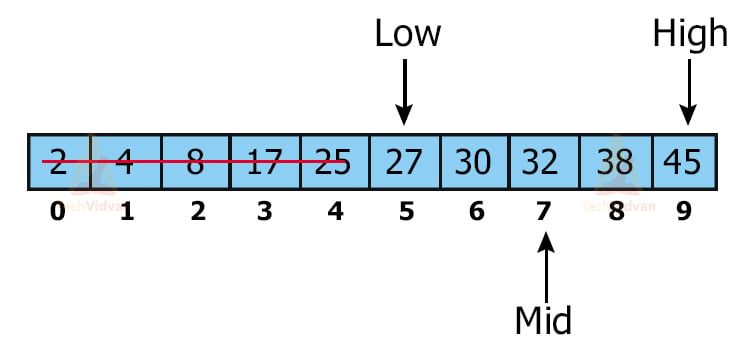
Step 2: Compare 38 with the middle element. 38 > 25 So, discard the first half.
Step 3: Select the send half of the array. For the second half, low = middle+1 as shown:
Step 4: Find the middle element of this smaller array which comes out to 32. Compare 38 with 32.
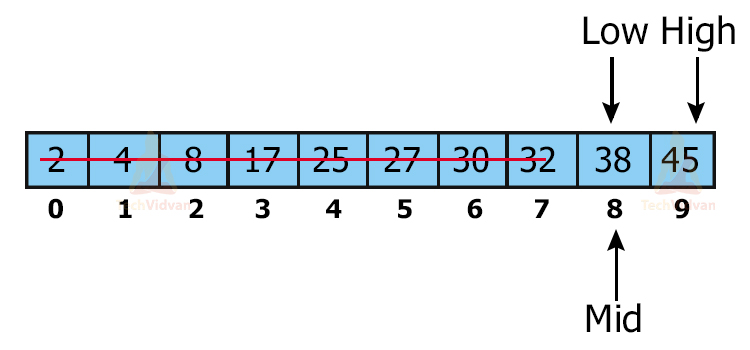
38 > 32 Thus, discard the first half of this array.
Step 5: Select the remaining half of the array by doing low = middle+1 as shown:
Finally, we have found 38 and thus the algorithm will halt here.
Output: 8.
Pseudo-code for Binary Search
We can implement binary search in two ways:
1. Iterative approach
2. Recursive approach (Using divide and conquer)
The pseudo-code for binary search is given as follows:
Procedure Binary_Search(int Arr[], n) //Arr is an array of length n
key := value to be searched
Set low = 1
Set high = n
while x not found
if high < low
Display x does not exist
EXIT.
set middle = low + (high - low) / 2
if Arr[mid] < key
set low = middle + 1
if Arr[middle] > key
set high = middle - 1
if Arr[middle] = key
Display x found at location middle
EXIT.
end while
end procedure
Binary Search Algorithm:
1. Using Iterative approach:
Step 1: Set low = first_index, high = last_index, location = -1
Step 2: Repeat steps 3 and 4 while low <= high
Step 3: set middle = (low + high)/2
Step 4:
if Arr[middle] == key
set loc = middle
Display “The element to be searched is present at location: “ + loc
go to step 6
else if Arr[mid] < key
set low = middle + 1
else
set high = middle - 1
[end if]
[end loop]
Step 5:
if loc == -1
print "Element to be searched is not present in the array"
[end of if]
Step 6: Stop
2. Using Recursive approach:
int Binary_Search(Arr[], key, low, high)
middle = (low + high) / 2
if key == Arr[middle]
return mid
else if key > Arr[middle]
return Binary_Search(Arr[], key, middle+1, high)
else
return Binary_Search(Arr[], key, low, middle-1)
Implementation of Linear Search in C:
Iterative code:
int Binary_Search(int Arr[], int low, int high, int key)
{
while (low <= high) {
int middle = low + (high - low) / 2;
if (Arr[middle] == key)
return middle;
if (Arr[middle] < key)
low = middle + 1;
else
high = middle - 1;
}
return -1;
}
int main(void)
{
int arr[] = {2, 4, 8, 17, 25, 27, 32, 38, 45};
int len = sizeof(arr) / sizeof(arr[0]);
int key = 38;
int result = Binary_Search(arr, 0, len-1, key);
if(result == -1)
printf("Element not found");
else
printf("Element found at index: %d",result+1);
return 0;
}
Recursive code:
#include <stdio.h>
int Binary_Search(int Arr[], int low, int high, int key)
{
if (high >= low) {
int middle = low + (high - low) / 2;
if (Arr[middle] == key)
return middle;
if (Arr[middle] > key)
return Binary_Search(Arr, low, middle-1, key);
return binarySearch(Arr, middle+1, high, key);
}
return -1;
}
int main(void)
{
int arr[] = {2, 4, 8, 17, 25, 27, 32, 38, 45};
int len = sizeof(arr) / sizeof(arr[0]);
int key = 38;
int result = Binary_Search(arr, 0, len-1, key);
if(result == -1)
printf("Element not found in the array");
else
printf("Element is found at location: %d ",result+1);
return 0;
}
Binary Search implementation in C++
Iterative code:
#include <bits/stdc++.h>
using namespace std;
int Binary_Search(int Arr[], int low, int high, int key)
{
while (low <= high) {
int middle = low + (high - low) / 2;
if (Arr[middle] == key)
return middle;
if (Arr[middle] < key)
low = middle + 1;
else
high = middle - 1;
}
return -1;
}
int main(void)
{
int arr[] = {2, 4, 8, 17, 25, 27, 32, 38, 45};
int len = sizeof(arr) / sizeof(arr[0]);
int key = 38;
int result = Binary_Search(arr, 0, len - 1, key);
if(result == -1)
cout << "Element not found" ;
else
cout << "Element found at index " << result+1;
return 0;
}
Recursive code:
#include <bits/stdc++.h>
using namespace std;
int Binary_Search(int Arr[], int low, int high, int key)
{
if (high >= low) {
int middle = low + (high - low) / 2;
if (Arr[middle] == key)
return middle;
if (Arr[middle] > key)
return Binary_Search(Arr, low, middle-1, key);
return Binary_Search(Arr, middle+1, high, key);
}
return -1;
}
int main(void)
{
int arr[] = {2, 4, 8, 17, 25, 27, 32, 38, 45};
int key = 38;
int len = sizeof(arr) / sizeof(arr[0]);
int result = Binary_Search(arr, 0, len - 1, key);
if(result == -1)
cout << "Element not found in the array" ;
else
cout << "Element found at location: " << result+1;
return 0;
}
Implementation of Binary Search in Java:
Iterative code:
public class BinarySearch {
int Binary_Search(int Arr[], int key)
{
int low = 0, high = Arr.length - 1;
while (low <= high) {
int middle = low + (high - low) / 2;
if (Arr[middle] == key)
return middle;
if (Arr[middle] < key)
low = middle + 1;
else
high = middle - 1;
}
return -1;
}
public static void main(String args[])
{
BinarySearch obj = new BinarySearch();
int Arr[] = {2, 4, 8, 17, 25, 27, 32, 38, 45};
int key = 38;
int result = obj.Binary_Search(Arr, key);
if (result == -1)
System.out.println("Element not found");
else
System.out.println("Element found at index: " + (result+1));
}
}
Recursive code:
public class BinarySearch {
int Binary_Search(int Arr[], int low, int high, int key)
{
if (high >= low) {
int middle = low + (high - low) / 2;
if (Arr[middle] == key)
return middle;
if (Arr[middle] > key)
return Binary_Search(Arr, low, middle-1, key);
return Binary_Search(Arr, middle+1, high, key);
}
return -1;
}
public static void main(String args[])
{
BinarySearch obj = new BinarySearch();
int Arr[] = {2, 4, 8, 17, 25, 27, 32, 38, 45};
int len = Arr.length;
int key = 38;
int result = ob.Binary_Search(Arr, 0, len-1, key);
if (result == -1)
System.out.println("Element not found");
else
System.out.println("Element found at index: " + result+1);
}
}
Binary Search implementation in Python:
Iterative code:
def Binary_Search(Arr, low, high, key):
while low <= high:
middle = low + (high - low)//2
if Arr[middle] == key:
return middle
elif Arr[middle] < key:
low = middle + 1
else:
high = middle - 1
return -1
list = [2, 4, 8, 17, 25, 27, 32, 38, 45]
key = 38
result = Binary_Search(list, 0, len(list)-1, key)
if result == -1:
print ("Element not found")
else:
print ("Element found at location: % d" % (result+1))
Recursive code:
def Binary_Search (Arr, low,high, key):
if high >= low:
middle = low + (high - low) // 2
if Arr[middle] == key:
return key
elif arr[middle] > key:
return Binary_Search(Arr, low, middle-1, key)
else:
return Binary_Search(Arr, middle + 1, high, key)
else:
return -1
list = [2, 4, 8, 17, 25, 27, 32, 38, 45]
key = 38
result = Binary_Search(list, 0, len(list)-1, key)
if result != -1:
print ("Element foubd at location % d" % (result+1))
else:
print ("Element not found")
Complexity of Binary Search
Binary Search Time complexity:
| Case | Complexity |
| Best case | O(1) |
| Average case | O(log n) |
| Worst case | O(log n) |
Binary Search Space complexity:
In the worst case, the space complexity is O(1).
Linear Search v/s Binary Search
| Linear search | Binary search |
| It follows a sequential approach. | This follows a divide and conquer approach. |
| It works well on unsorted data. | To apply binary search, data has to be sorted. |
| Its worst-case time complexity is O(n). | Its worst-case time complexity is O(log n) |
| It is slower in comparison to binary search. | It is more efficient than linear search. |
| In linear search, we compare an element with every other element. | In binary search, we don’t compare an element with all other elements. We leave a few comparisons. |
| We prefer linear search only for small-sized data. | It is preferred for large-sized data. |
| We can implement linear search on all linear data structures like arrays and linked lists. | We can implement binary search only on those data structures that permit 2-way traversal. |
Applications of Binary Search
1. It is internally used in the inbuilt libraries of programming languages such as C, C++ and Java.
2. It helps to pinpoint the position of error during debugging of a particular code.
Conclusion
Binary search is a searching technique that follows the divide and conquer strategy. It is more efficient in comparison to other searching algorithms.
In this article, we have covered the working of binary search, its implementation in various programming languages as well as its application in the programming world. We have also discussed how binary search is different from linear search.