Binary Search Tree in Data Structure
A binary search tree(BST) is a special type of binary tree and is also known as a sorted or ordered binary tree. In a binary search tree:
- The value of the left node is less than the value of the parent node.
- The value of the right node is greater than the value of the parent node.
Thus, in a binary search tree, all the values in the left subtree are smaller than the value at the root node and all the values in the right subtree are larger than the value at the root node. A binary search tree usually does not have any duplicate nodes. The following tree represents a binary search tree:
The benefit of using a binary search tree over a binary tree is that search operation can be performed in O(log n) time because of ordering in the BST. A binary search tree performs better in search, insert and delete operations as compared to a simple binary tree.
Representation of Binary Search Tree:
Like a binary tree, a binary search tree is also a collection of nodes where each parent node can have a maximum of two children. A node in a binary search tree has the following structure:
struct Node {
int key;
struct Node *left_child;
struct Node *right_child;
};
Operations on Binary Search Tree:
1. Searching
2. Insertion
3. Deletion
4. Traversal
The traversal operation is of three different types:
1. Pre-order traversal: It will traverse the root first, then the left child and at last the right child.
2. Post-order traversal: It will traverse the left subtree first, then root and then the right subtree.
3. Inorder traversal: It will traverse the left subtree, then root and then the right subtree.
Search Operation in a BST:
This operation is used to search a key value in a binary search tree. Searching in a BST is very efficient because the values are ordered. While searching for a value, we first compare it with the root node. If the value is less than the root node, then it must surely be present in the left subtree. If the value is greater than the root node, then it will be present in the right subtree. Thus, we will traverse the subtrees accordingly until we reach the desired location. The search operation takes O(log n) time.
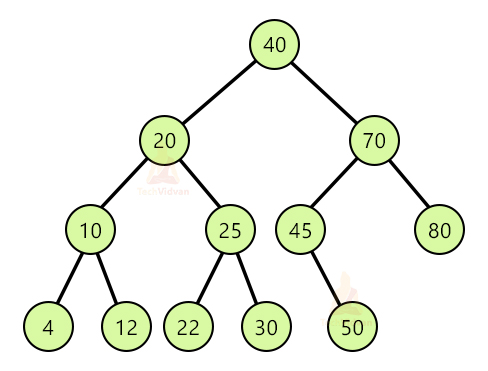
Let us understand with the help of the following example:
Suppose we wish to search 10. We will start from the root node i.e.40. The value of 40 is more than the value of 10, therefore 10 must be present in the left subtree. Thus, we will discard the right subtree and start traversing the left subtree in the same manner. Now we reach the node having a value of 20. Again 20>10, so will discard the right subtree and move further in the left subtree. Moving this direction, we finally get our desired value i.e. 10. This is how search operation works in a binary search tree.
Algorithm for Searching in a BST:
if (root == NULL)
return NULL;
if (num == root->key)
return root->key;
if (num < root->key)
return Binary_search(root->left)
if (num > root->key)
return Binary_search(root->right)
Pseudo-code for Searching in a BST:
struct Node* Binary_search(int key){
struct Node *current = Root;
while(current->key != key){
if(current != NULL) {
display(current->key);
if(current->key > key){
current = current->left_child;
else
current = current->right_child;
if(current == NULL){
return NULL;
}
}
}
return current;
}
Insertion in a Binary Search Tree:
Insertion operation is used to insert values inside the tree. While inserting a value, we need to take care that the order of the binary search tree is not disturbed. Thus, every value must be inserted at its right place according to its order.
While performing the insert operation, we first compare the value to be inserted with the root node value. If the value is less than the root node, we place it in the left subtree. If the value is more than the root node, we will place it in the right subtree. For inserting a value at the right place, we need to search the correct location first.
Algorithm for Insertion in a BST:
if (Node == NULL)
return create_node(key)
if (key < Node->key)
Node->left_child = insert(Node->left_child, key);
else if (key > Node->key)
Node->right_child = insert(Node->right_child, key);
return Node;
Pseudo-code for Insertion in a BST:
procedure insertion(int key):
struct Node *temp = (struct Node*) malloc(sizeof(struct Node));
struct Node *current;
struct Node *parent;
temp->key = key;
temp->left_child = NULL;
temp->right_child = NULL;
if(Root == NULL)
Root = temp;
else:
current = Root;
parent = NULL;
END else
while(1) {
parent = current;
if(key < parent->key):
current = current->left_child;
if(current == NULL):
parent->left_child = temp;
return;
END if
END if
else:
current = current->right_child;
if(current == NULL):
parent->right_child = temp;
return;
END if
END else
END while
END procedure
Deletion in a BST
The deletion operation includes removing a node from the BST. For performing the deletion operation, first, we have to search the location of the element. The node could be a leaf node, an internal node with one child or an internal node with two children. Let us discuss all the different cases.
Case 1: When the node is a leaf node:
If we wish to delete a leaf node, we will simply remove it without affecting the other nodes of the tree and set it to NULL. For deleting a node, we need to know its parent node.
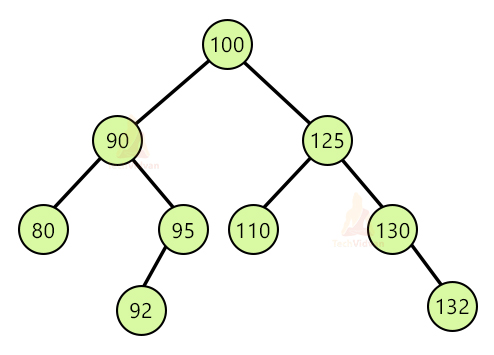
Consider the following example:
Suppose we wish to delete 70 from this tree. We will first go to the root node and compare the value of 70 to it. As 70<100, therefore, we will start looking for 70 in the left subtree. In the left subtree, we first encounter 90 which is again greater than 70. So, we will again traverse the left part of the subtree. Again 70<80, therefore we traverse the left subtree. Finally, after this step, we reach 70.
We will delete 70 from the tree and set the left pointer of 80 i.e. the parent of 70 to NULL. Thus, two operations are happening here: removing 70 from the tree and setting the left pointer of 80 to NULL. In case of deletion from the leaf node, if the height of the tree is h, then the number of comparisons will be h+1.
Case 2: Deletion of an internal node having one child:
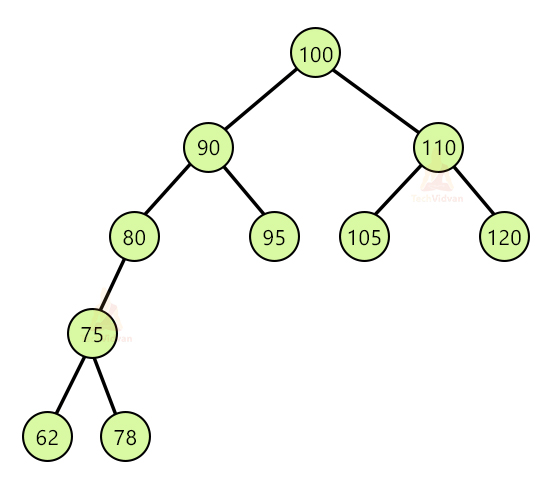
Let the binary search tree be:
Here, 80 has only 1 child. Suppose we wish to delete 80 from the tree. To delete 80, we need to know the inorder traversal of the tree. In this case, the inorder traversal is: 62, 75, 78, 80, 90, 95, 100, 105, 110, 120.
Once we remove 80, the inorder traversal will be: 62, 75, 78, 90, 95, 100, 105, 110, 120. Thus, after removing 80, the tree will be:
Case 3: Deletion of an internal node having two child nodes:
To delete an internal node having 2 child nodes, first find the in order successor of the node to be deleted and then swap it with the node. Now we have our node at the leaf position, therefore, we will simply remove it.
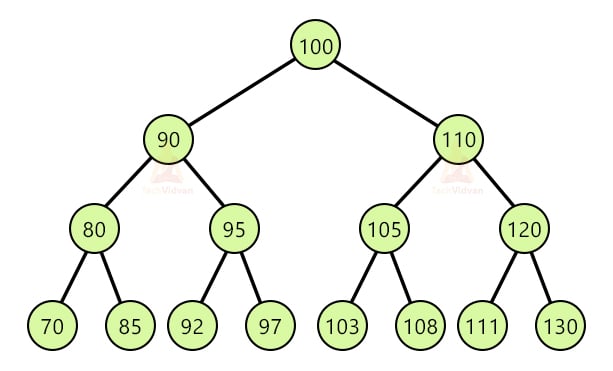
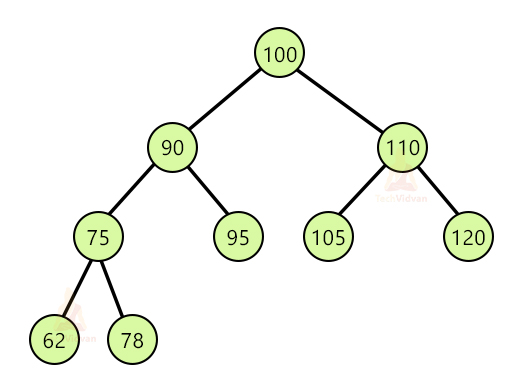
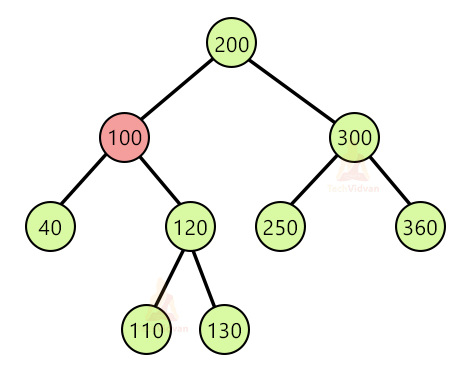
For example, consider the following tree:
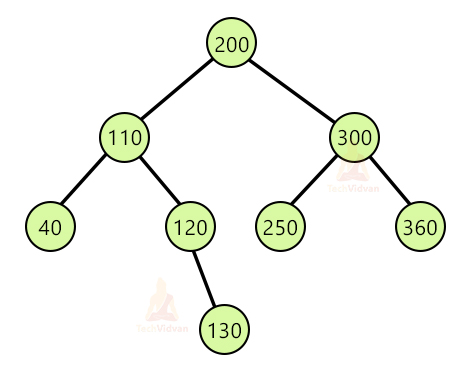
Suppose we wish to remove 100 from the tree. We will find the inorder successor of 100 which comes out to be 110. We will swap 110 and 100 and then delete 100. Thus, the final tree will be:
Implementation of Binary Search Tree in C:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int key;
struct node *left_child, *right_child;
};
struct Node *new_node(int value) {
struct Node *temp = (struct Node *)malloc(sizeof(struct Node));
temp->key = value;
temp->left_child = temp->right_child = NULL;
return temp;
}
void inorder_traversal(struct Node *Root) {
if (Root != NULL) {
inorder_traversal(Root->left_child);
printf("%d -> ", Root->key);
inorder_traversal(Root->right_child);
}
}
struct Node *insertion(struct Node *Node, int key) {
if (Node == NULL)
return new_node(key);
if (key < Node->key)
Node->left_child = insertion(Node->left_child, key);
else
Node->right_child = insertion(Node->right_child, key);
return node;
}
struct Node *min_value(struct Node *Node) {
struct Node *current = Node;
while (current && current->left_child != NULL)
current = current->left_child;
return current;
}
struct Node *deletion(struct Node *Root, int key) {
if (Root == NULL)
return Root;
if (key < Root->key)
Root->left_child = deletion(Root->left_child, key);
else if (key > Root->key)
Root->right_child = deletion(Root->right_child, key);
else {
if (Root->left_child == NULL) {
struct Node *temp = Root->right_child;
free(Root);
return temp;
}
else if (Root->right_child == NULL) {
struct Node *temp = Root->left_child;
free(Root);
return temp;
}
struct Node *temp = min_value(Root->right_child);
Root->key = temp->key;
Root->right_child = deletion(Root->right_child, temp->key);
}
return Root;
}
int main() {
struct Node *root = NULL;
root = insert(root, 200);
root = insert(root, 100);
root = insert(root, 40);
root = insert(root, 120);
root = insert(root, 130);
root = insert(root, 300);
root = insert(root, 250);
root = insert(root, 360);
root = insert(root, 110);
printf("Inorder traversal: ");
inorder_traversal(root);
printf("\nAfter deleting 10\n");
root = deletion(root, 100);
printf("Inorder traversal: ");
inorder_traversal(root);
}
Binary Search Tree Implementation in C++:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int key;
struct node *left_child, *right_child;
};
struct Node *new_node(int value) {
struct Node *temp = (struct Node *)malloc(sizeof(struct Node));
temp->key = value;
temp->left_child = temp->right_child = NULL;
return temp;
}
void inorder_traversal(struct Node *Root) {
if (Root != NULL) {
inorder_traversal(Root->left_child);
printf("%d -> ", Root->key);
inorder_traversal(Root->right_child);
}
}
struct Node *insertion(struct Node *Node, int key) {
if (Node == NULL)
return new_node(key);
if (key < Node->key)
Node->left_child = insertion(Node->left_child, key);
else
Node->right_child = insertion(Node->right_child, key);
return node;
}
struct Node *min_value(struct Node *Node) {
struct Node *current = Node;
while (current && current->left_child != NULL)
current = current->left_child;
return current;
}
struct Node *deletion(struct Node *Root, int key) {
if (Root == NULL)
return Root;
if (key < Root->key)
Root->left_child = deletion(Root->left_child, key);
else if (key > Root->key)
Root->right_child = deletion(Root->right_child, key);
else {
if (Root->left_child == NULL) {
struct Node *temp = Root->right_child;
free(Root);
return temp;
}
else if (Root->right_child == NULL) {
struct Node *temp = Root->left_child;
free(Root);
return temp;
}
struct Node *temp = min_value(Root->right_child);
Root->key = temp->key;
Root->right_child = deletion(Root->right_child, temp->key);
}
return Root;
}
int main() {
struct Node *root = NULL;
root = insertion(root, 200);
root = insertion(root, 100);
root = insertion(root, 40);
root = insertion(root, 120);
root = insertion(root, 130);
root = insertion(root, 300);
root = insertion(root, 250);
root = insertion(root, 360);
root = insertion(root, 110);
printf("Inorder traversal: ");
inorder_traversal(root);
printf("\nAfter deleting 10\n");
root = deletion(root, 100);
printf("Inorder traversal: ");
inorder_traversal(root);
}
Implementation of Binary Search Tree in Java:
class BinarySearchTree {
class Node {
int key;
Node left_child, right_child;
public Node(int value) {
key = value;
left_child = right_child = null;
}
}
Node root;
BinarySearchTree() {
root = null;
}
void insertion(int key) {
root = insert_key(root, key);
}
Node insert_key(Node root, int key) {
if (root == null) {
root = new Node(key);
return root;
}
if (key < root.key)
root.left_child = insert_key(root.left_child, key);
else if (key > root.key)
root.right_child = insert_key(root.right_child, key);
return root;
}
void inorder_traversal() {
inorder_rec(root);
}
void inorder_rec(Node root) {
if (root != null) {
inorder_rec(root.left_child);
System.out.print(root.key + " -> ");
inorder_rec(root.right_child);
}
}
void deletion(int key) {
root = deletion(root, key);
}
Node delete_rec(Node root, int key) {
if (root == null)
return root;
if (key < root.key)
root.left_child = delete_rec(root.left_child, key);
else if (key > root.key)
root.right_child = deletion(root.right_child, key);
else {
if (root.left_child == null)
return root.right_child;
else if (root.right_child == null)
return root.left_child;
root.key = min_value(root.right_child);
root.right_child = delete_rec(root.right_child, root.key);
}
return root;
}
int min_value(Node root) {
int minv = root.key;
while (root.left_child != null) {
minv = root.left_child.key;
root = root.left_child;
}
return minv;
}
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
tree.insertion(200);
tree.insertion(100);
tree.insertion(40);
tree.insertion(120);
tree.insertion(130);
tree.insertion(300);
tree.insertion(250);
tree.insertion(360);
tree.insertion(110);
System.out.print("Inorder traversal: ");
tree.inorder_traversal();
System.out.println("\n\nAfter deleting 10");
tree.deletion(100);
System.out.print("Inorder traversal: ");
tree.inorder_traversal();
}
}
Implementation of BST in Python:
class Node:
def __init__(self, key):
self.key = key
self.left_child = None
self.right_child = None
def inorder_traversal(root):
if root is not None:
inorder_traversal(root.left_child)
print(str(root.key) + "->", end=' ')
inorder_traversal(root.right_child)
def insertion(Node, key):
if Node is None:
return Node(key)
if key < Node.key:
Node.left_child = insertion(node.left_child, key)
else:
node.right_child = insertion(node.right_child, key)
return Node
def min_value(node):
current = node
while(current.left_child is not None):
current = current.left_child
return current
def deletion(root, key):
if root is None:
return root
if key < root.key:
root.left_child = deletion(root.left_child, key)
elif(key > root.key):
root.right_child = deletion(root.right_child, key)
else:
if root.left_child is None:
temp = root.right_child
root = None
return temp
elif root.right_child is None:
temp = root.left_child
root = None
return temp
temp = min_value(root.right_child)
root.key = temp.key
root.right_child = deletion(root.right_child, temp.key)
return root
root = None
root = insertion(root, 200)
root = insertion(root, 100)
root = insertion(root, 40)
root = insertion(root, 120)
root = insertion(root, 130)
root = insertion(root, 300)
root = insertion(root, 250)
root = insertion(root, 360)
root = insertion(root, 110)
print("Inorder traversal: ", end=' ')
inorder_traversal(root)
print("\nDelete 100")
root = deletion(root, 10)
print("Inorder traversal: ", end=' ')
inorder_traversal(root)
Complexity Analysis of Binary Search Tree:
Consider a tree having n nodes. Then, the time complexity of Binary Search Tree will be:
| Scenario/Operation | Search | Insert | Delete |
| Worst case | O(n) | O(n) | O(n) |
| Average case | O(log n) | O(log n) | O(log n) |
| Best case | O(log n) | O(log n) | O(log n) |
The space complexity in all operations is O(n).
Advantages of Binary Search Tree:
- Searching is more efficient as compared to a simple binary tree.
- The insertion and deletion operations are faster in a binary search tree in comparison to arrays and linked lists.
- At each step, the binary search tree removes half the subtree and this makes it work faster.
Applications of Binary Search Tree:
- It is used in multi-level indexing in the database management system.
- Used in UNIX kernel to manage virtual memory areas
- Used in dynamic sorting of elements.
Conclusion
In this article, we have seen the working of various operations such as insertion, deletion and searching in a binary search tree. We have also gone through the complexity analysis and various applications of a BST.