TechVidvan

Binary Tree Data Structure

A binary tree is a tree in which every node has either 0, 1 or 2 children. If it has zero children, it means the node is a leaf node. If the node has 1 or 2 children, it means the node is an internal node. Each node of the binary tree has 3 components:

1. Data value at the node
2. Pointer to the left child
3. Pointer to the right child

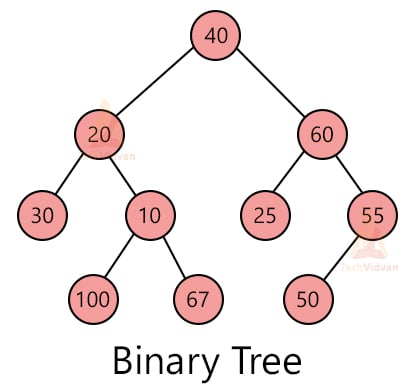
The following diagram shows an example of a binary tree.

Binary tree Example

Properties of Binary Trees:

1. Maximum number of nodes in a binary tree:

If the height of the binary tree is h, then the maximum total number of nodes will be 20 + 21 + 22 + ……….+ 2h-1 which will give out 2h-1 number of nodes.

Thus, the maximum number of nodes in a binary tree of height h is 2h-1.

2. Maximum number of nodes at a particular level:

In the case of the root node, level = 0. The number of nodes at level=0 is 20. At level=1, the number of nodes = 21.
Similarly, at level = l, the number of nodes = 2l.

3. Number of levels with given leaves:

For a binary tree, the number of leaves will be maximum when all the levels are completely filled.

Let the number of leaves be L. Then, L ≤ 2l-1(From point 2)

l = log2 L + 1. Here, l = minimum number of levels.

4. Minimum possible height or level:

If the height of the root node is taken to be zero, then the minimum possible height comes out to be log2(N+1) – 1.

5. Number of leaf nodes when a binary tree has 0 or 2 nodes:

If the binary tree has either 0 nodes or 2 nodes, then the number of leaf nodes is always one more than the number of internal nodes i.e. nodes with 2 children.

Let L = Number of leaf nodes And let T = Number of internal nodes with two children.

Then, L = T + 1.

Need for Binary Trees:

1. Binary trees help to implement other data structures such as heaps and priority queues.

2. A binary search tree, a special case of a binary tree is very efficient and fast to search an element from a huge set.

3. Binary trees also play an important role in databases to implement indexing with the help of B-trees.

Types of Binary Trees:

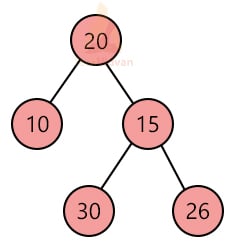
1. Full binary tree:

In a full binary tree, every internal node has either zero children or 2 children. The following diagram shows an example of a full binary tree.

Full Binary Tree

A full binary tree has the following properties:

  • The maximum number of nodes in a full binary tree is 2h+1 -1.
  • The number of leaf nodes is always one more than the number of internal nodes i.e. L = T + 1.
  • The minimum height of a full binary tree is log2(n+1) – 1.
  • The minimum number of nodes in a full binary tree is 2*h-1.
  • The maximum height of a full binary tree is (n+1)/2.

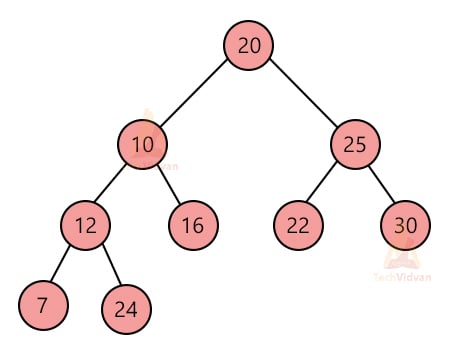
2. Complete binary tree:

A complete binary tree is a tree in which the nodes are filled level-wise i.e. we can’t go to the next level of the tree until the previous level is completely filled. We fill the nodes from left to right at each level.

Complete Binary Tree

A complete binary tree has the following properties:

  • The maximum number of nodes in a complete binary tree is 2h+1 -1.
  • The minimum number of nodes in a complete binary tree is 2h.
  • The minimum height of a complete binary tree is log2(n+1) – 1.
  • The maximum height of a complete binary tree is (n+1)/2.

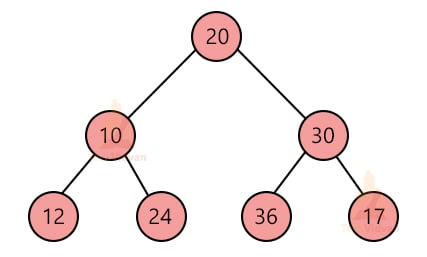
3. Perfect binary tree:

It is a tree in which all the leaf nodes have the same level and all the internal nodes have exactly two child nodes. The following diagram shows a perfect binary tree.

Perfect Binary Tree

In a perfect binary tree,

  • The number of leaf nodes is always one more than the number of internal nodes i.e. L = T + 1. Here, L is the number of leaf nodes and T is the number of internal nodes.
  • If the height of the tree is h, then the number of nodes in a perfect binary tree is 2h-1.

4. Balanced binary tree:

A tree is said to be balanced if its complexity is not more than O(log n). For example, an AVL tree, a red-black tree and a splay tree are balanced trees. An AVL tree maintains balance with the help of a balancing factor such that the difference between the height of the left and the right sub-tree never exceeds 1. The red-black tree ensures that there are no adjacent red nodes and the number of black nodes on the right and left subtree are equal.

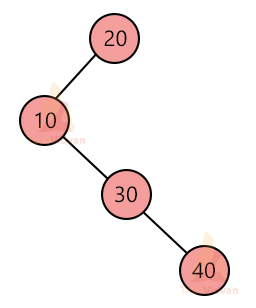
5. Pathological tree:

It is also known as a degenerate tree. It has a single child at each level. The child could be either left or right. Performance-wise, it behaves exactly like a linked list. The following diagram shows an example of a pathological or a degenerate tree.

Pathological Tree

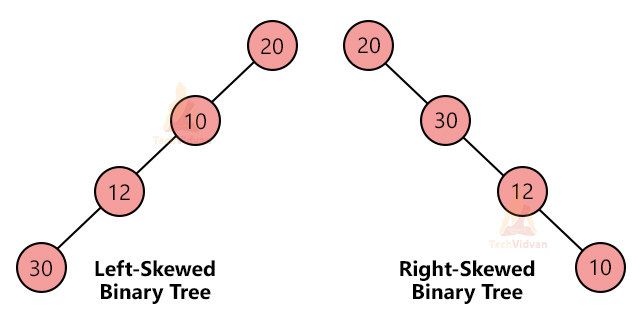
6. Skewed binary tree:

A skewed binary tree is one that is skewed on one side either right or left i.e. one side is dominated in a skewed tree. It could be either left-skewed or right-skewed. A skewed binary tree starts behaving like a linear data structure leading to very high complexity.

Skewed Binary Tree

Memory Representation of a Binary tree:

The most basic component of any tree is a node. A node is a heterogeneous data type consisting of a key and two pointers to the structure of the same type i.e. it represents a self-referencing structure.

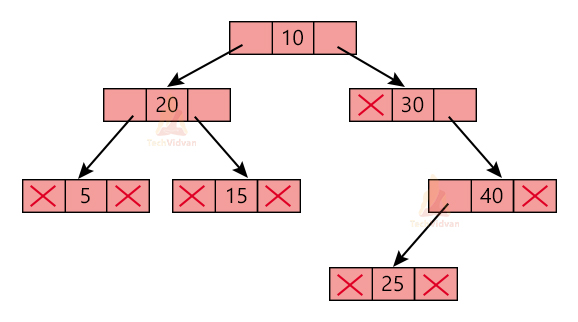
The following diagram is a memory representation of the tree data structure.

Memory Representation of Binary Tree

Each node contains 3 fields: a data item, a pointer to the left child and a pointer to the right child. The first and the third fields store addresses of other nodes and help to link the tree with other nodes. The second field contains the actual value of the node.

Declaration of a Binary Tree:

We can define this structure of the tree in a programming language using a heterogeneous data type such as struct as shown:

struct Node  
{  
    int key;  
    struct Node *left_child;  
    struct Node *right_child;   
}

Creating Nodes in a Binary Tree:

The following code explains the procedure to create nodes in a binary tree:

struct Node *root;
struct Node *node1 = NULL;
struct Node *node2 = NULL;
struct Node *node3 = NULL;

node1 = malloc(sizeof(struct Node));
node2 = malloc(sizeof(struct Node));
node3 = malloc(sizeof(struct Node));

node1->value = 10;
node2->value = 20;
node3->value = 30;

node1->left = node2;
node1->right = node3;
node2->left = NULL;
node2->right = NULL;
node3->left = NULL;
node3->right = NULL;

root = node1;

Implementation of Binary Tree in C:

#include <stdio.h>
#include <stdlib.h>
struct Node {
  int key;
  struct node* left;
  struct node* right;
};

struct Node* new_node(int key)
{
  struct Node* Node = (struct Node*)malloc(sizeof(struct Node));
  Node->key = key;
  Node->left = NULL;
  Node->right = NULL;
  return (Node);
}

int main()
{
  struct Node* root = new_node(20);
  root->left = new_node(15);
  root->right = new_node(32);
  root->left->left = new_node(40);
  root->left->right = new_node(45);
  root->right->left = new_node(24);
  return 0;
}

Binary Tree Implementation in C++

#include <bits/stdc++.h>
struct Node {
  int key;
  struct node* left;
  struct node* right;
};

struct Node* new_node(int key)
{
  struct Node* Node = (struct Node*)malloc(sizeof(struct Node));
  Node->key = key;
  Node->left = NULL;
  Node->right = NULL;
  return (Node);
}

int main()
{
  struct Node* root = new_node(20);
  root->left = new_node(15);
  root->right = new_node(32);
  root->left->left = new_node(40);
  root->left->right = new_node(45);
  root->right->left = new_node(24);
  return 0;
}

Binary Tree Implementation in Java:

class Node
{
  int key;
  Node left, right;

  public Node(int value)
  {
    key = value;
    left = right = null;
  }
}

class Binary_Tree
{
  Node root;
  Binary_Tree(int key)
  {
    root = new Node(key);
  }

  Binary_Tree()
  {
    root = null;
  }

  public static void main(String[] args)
  {
    BinaryTree tree = new BinaryTree();
    tree.root = new Node(20);
    tree.root.left = new Node(15);
    tree.root.right = new Node(32);
    tree.root.left.left = new Node(40);
    tree.root.left.right = new Node(45);
    tree.root.right.left = new Node(24);
  }
}

Implementation of Binary Tree in Python:

class Node:
  def __init__(self,key):
    self.left = None
    self.right = None
    self.value = key

root = Node(20)
root.left	 = Node(15);
root.right	 = Node(32);
root.left.left = Node(40);
root.left.right = Node(45);
root.right.left	 = Node(24);

Applications of Binary Trees:

  • Used in writing syntax trees for compilers
  • Helps to access data easily and more quickly
  • Heap data structure is implemented using a full binary tree
  • Used in routing algorithms

Conclusion:

Binary trees are a very efficient data structure especially when we wish to store data in a non-linear fashion. They are easy to implement and quick to access. In this article, we have gone through their various properties, types, and applications. We have also seen its implementation in various programming languages.