Breadth First Search in Data Structure
Traversal means to visit each node of a graph. For graphs, there are two types of traversals: Depth First traversal and Breadth-First traversal. In this article, we are going to study Breadth-first traversal or BFS in detail.
What is Breadth First Search?
Breadth First Search is a traversal technique in which we traverse all the nodes of the graph in a breadth-wise motion. In BFS, we traverse one level at a time and then jump to the next level.
In a graph, the traversal can start from any node and cover all the nodes level-wise. The BFS algorithm makes use of the queue data structure for implementation. In BFS, we always reach the final goal state (which was not always the case for DFS).
Algorithm for BFS:
Step 1: Choose any one node randomly, to start traversing.
Step 2: Visit its adjacent unvisited node.
Step 3: Mark it as visited in the boolean array and display it.
Step 4: Insert the visited node into the queue.
Step 5: If there is no adjacent node, remove the first node from the queue.
Step 6: Repeat the above steps until the queue is empty.
Working of Breadth First Search:
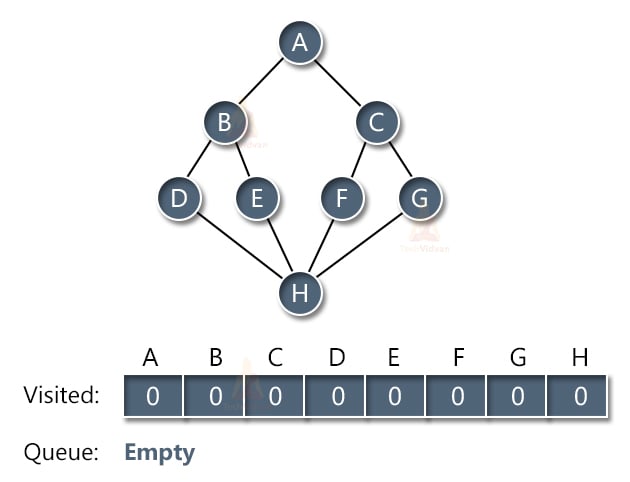
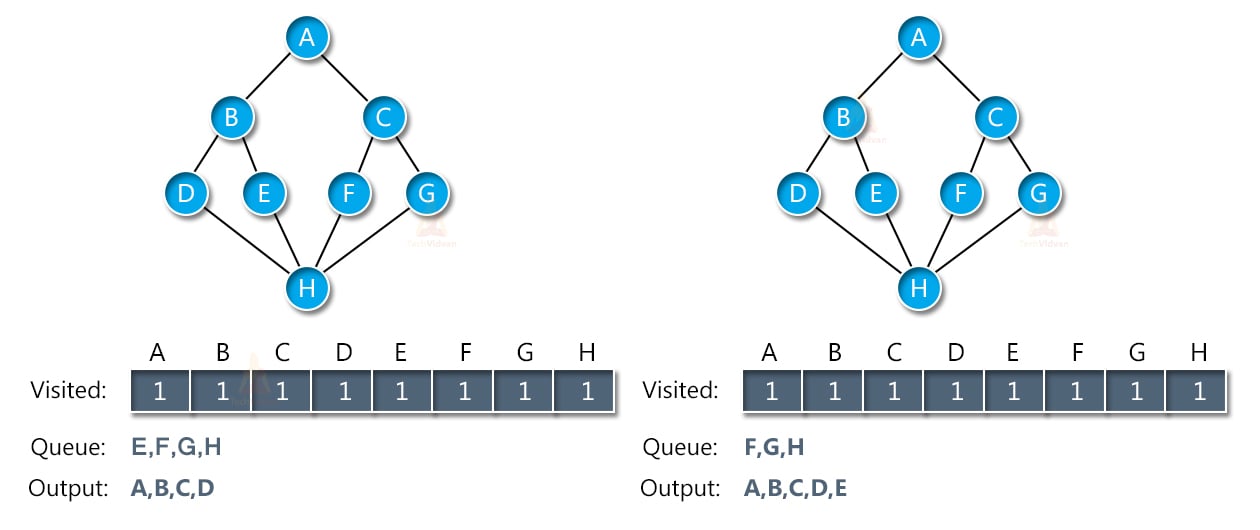
Consider the following graph having 8 nodes named as A, B, C, D, E, F, G and H as shown:
Initially, the queue will be empty.
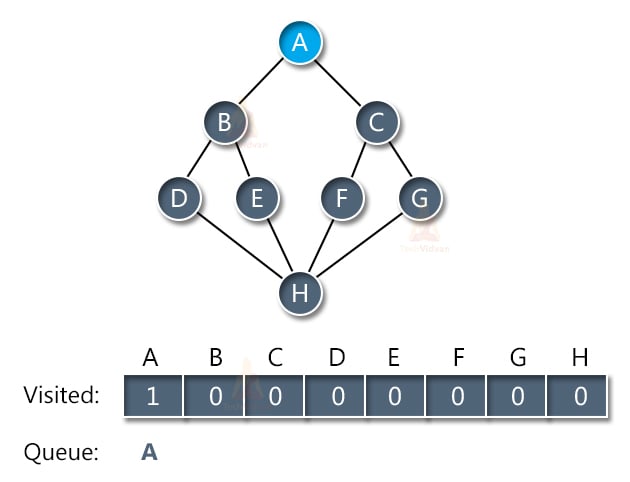
Let us start traversing the graph from node A. Once we visit node A, we mark it as visited and also place it inside the queue as shown:
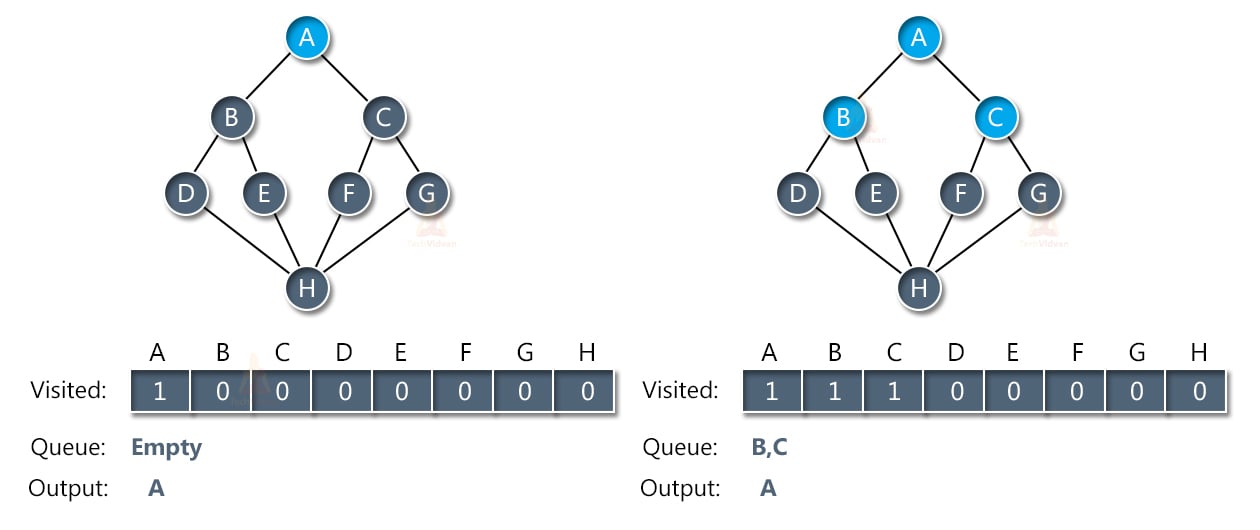
The next step is to traverse its adjacent nodes i.e. B and C and place them inside the queue. When we place the adjacent node of A in the queue, we will remove A from the queue and display it in the output array as shown:
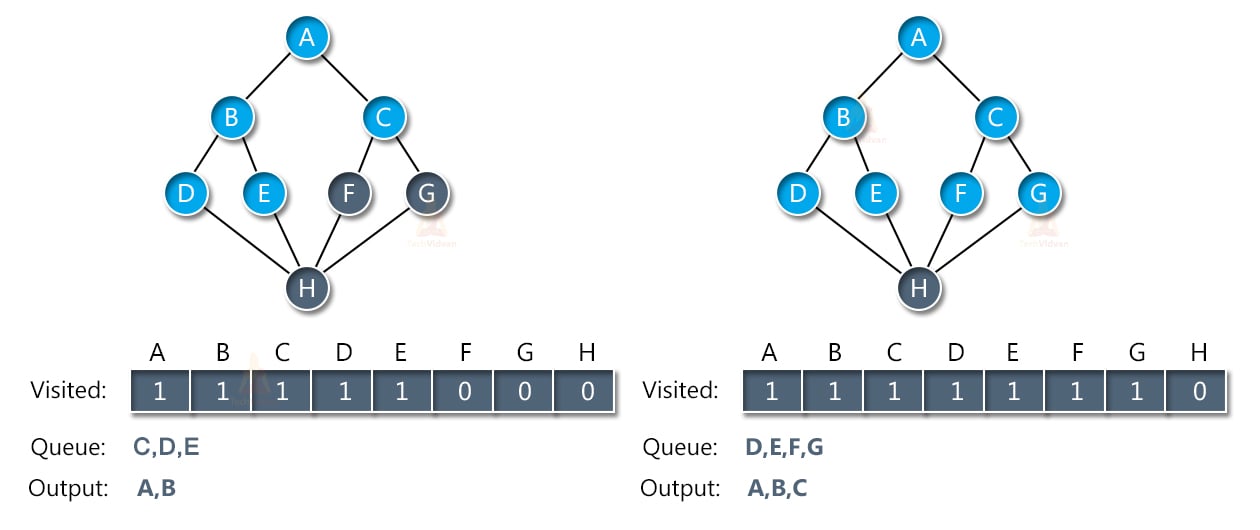
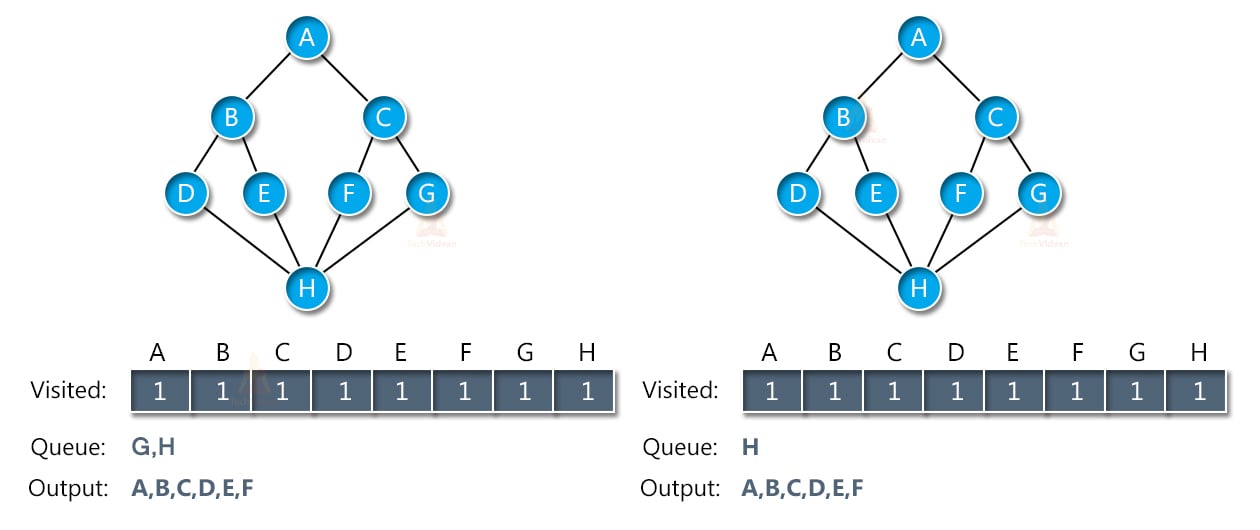
Next, we don’t have any more adjacent nodes for A. therefore, we will remove node B from the queue and place its adjacent nodes into the queue. Similarly, we will traverse the nodes of C and put them into the queue.
The next adjacent node is node H. thus, we will traverse that as well and place it in the queue. Once all the nodes have entered the queue, we will start removing them from the queue and putting them into the output array.
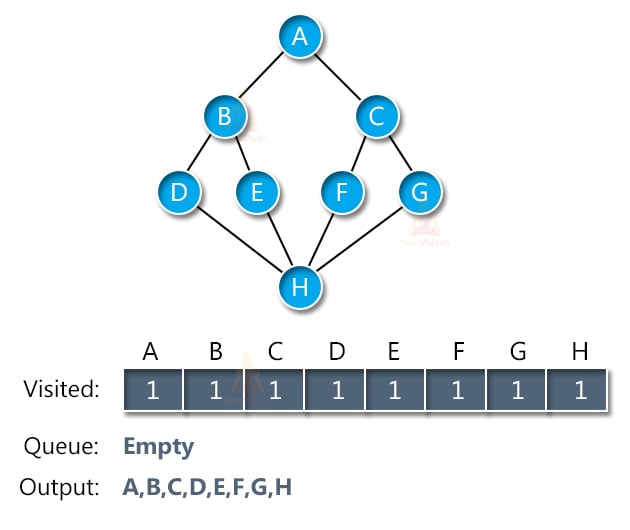
Thus, slowly the queue starts decreasing in size and the output array will be full as shown:
In this way, we will get the output of BFS to be A→B→C→D→E→F→G→H.
Pseudo-code for BFS:
procedure BFS(Graph, root) is
Let root = explored
Queue.enqueue(root)
while(Queue is not empty):
v := Queue.dequeue()
if v == goal:
return v
for all edges from v to w in Graph.adjacentEdges(v):
if w is not labeled as explored:
label w as explored
Queue.enqueue(w)
END for
END while
END BFS
Implementation of BFS in C:
#include <stdio.h>
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Node{
char label;
bool visited;
};
int Queue[MAX];
int Rear = -1;
int Front = 0;
int queue_item_count = 0;
struct Node* lst_Nodes[MAX];
int adj_matrix[MAX][MAX];
int node_count = 0;
void insert(int data) {
Queue[++Rear] = data;
queue_item_count++;
}
int remove_data() {
queue_item_count--;
return Queue[Front++];
}
bool isQueueEmpty() {
return queue_item_count == 0;
}
void addNode(char label) {
struct Node* node = (struct Node*) malloc(sizeof(struct Node));
node->label = label;
node->visited = false;
lst_Nodes[node_count++] = node;
}
void addEdge(int start,int end) {
adj_matrix[start][end] = 1;
adj_matrix[end][start] = 1;
}
void display_node(int node_index) {
printf("%c ",lst_Nodes[node_index] -> label);
}
int get_adj_unvisited_node(int node_index) {
int i;
for(i = 0; i<node_count; i++) {
if(adj_matrix[node_index][i] == 1 && lst_Nodes[i]->visited == false)
return i;
}
return -1;
}
void BFS() {
int i;
lst_Nodes[0]->visited = true;
display_node(0);
insert(0);
int unvisited_node;
while(!isQueueEmpty()) {
int temp_node = remove_data();
while((unvisited_node = get_adj_unvisited_node(temp_node)) != -1) {
lst_Nodes[unvisited_node]->visited = true;
display_node(unvisited_node);
insert(unvisited_node);
}
}
for(i = 0; i<node_count; i++) {
lst_Nodes[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i<MAX; i++) {
for(j = 0; j<MAX; j++)
adj_matrix[i][j] = 0;
}
addVertex('A');
addVertex('B');
addVertex('C');
addVertex('D');
addVertex('E');
addEdge(0, 1);
addEdge(0, 2);
addEdge(0, 3);
addEdge(1, 4);
addEdge(2, 4);
addEdge(3, 4);
printf("\nBreadth First Search: ");
BFS();
return 0;
}
BFS Implementation in C++
#include<bits/stdc++.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
public:
Graph(int V);
void addEdge(int v, int w);
void BFS(int s);
};
Graph::Graph(int V)
{
this->V = V;
adjacent = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adjacent[v].push_back(w);
}
void Graph::BFS(int s)
{
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;
list<int> queue;
visited[s] = true;
queue.push_back(s);
list<int>::iterator i;
while(!queue.empty())
{
s = queue.front();
cout << s << " ";
queue.pop_front();
for (i = adjacent[s].begin(); i != adjacent[s].end(); ++i)
{
if (!visited[*i])
{
visited[*i] = true;
queue.push_back(*i);
}
}
}
}
int main()
{
Graph g(4);
g.addEdge(0, 2);
g.addEdge(0, 1);
g.addEdge(1, 3);
g.addEdge(2, 1);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "The Breadth First Traversal is: \n";
g.BFS(1);
return 0;
}
Implementation of Breadth First Search in Java:
import java.io.*;
import java.util.*;
class Graph
{
private int V;
private LinkedList<Integer> adjacent[];
Graph(int v)
{
V = v;
adjacent = new LinkedList[v];
for (int i=0; i<v; ++i)
adjacent[i] = new LinkedList();
}
void addEdge(int v,int w)
{
adjacent[v].add(w);
}
void BFS(int s)
{
boolean visited[] = new boolean[V];
LinkedList<Integer> queue = new LinkedList<Integer>();
visited[s]=true;
queue.add(s);
while (queue.size() != 0)
{
s = queue.poll();
System.out.print(s+" ");
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
{
visited[n] = true;
queue.add(n);
}
}
}
}
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 2);
g.addEdge(0, 1);
g.addEdge(1, 3);
g.addEdge(2, 1);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("The Breadth First Traversal is: ");
g.BFS(1);
}
}
Implementation of BFS in Python
class Graph:
def __init__(self):
self.graph = defaultdict(list)
def addEdge(self,u,v):
self.graph[u].append(v)
def BFS(self, s):
visited = [False] * (max(self.graph) + 1)
queue = []
queue.append(s)
visited[s] = True
while queue:
s = queue.pop(0)
print (s, end = " ")
for i in self.graph[s]:
if visited[i] == False:
queue.append(i)
visited[i] = True
g = Graph()
g.addEdge(0, 2)
g.addEdge(0, 1)
g.addEdge(1, 3)
g.addEdge(2, 1)
g.addEdge(2, 3)
g.addEdge(3, 3)
print ("The Breadth First Traversal is: ")
g.BFS(1)
Complexity of BFS
Time complexity: Since we are visiting all the nodes exactly once, therefore, the time complexity is O(V+E). Here, O(E) may vary between O(1) and O(V2). Thus, in the worst case, the time complexity of BFS is O(V2).
Space complexity: The space complexity of the BFS algorithm is O(V) where V denotes vertices/nodes of the graph.
Applications of Breadth First Search
- To find the shortest path between two edges when the path length is equivalent to the number of edges.
- To check whether a graph is bipartite or not
- To copy garbage collection by Cheney’s algorithm
- Used in unweighted graphs to find the minimum cost spanning tree
- To form peer-to-peer network connections
- To find neighboring locations in the GPS navigation system
- To detect cycle in an undirected graph
- To broadcast packets in a network
- To find all the nodes within one connected component in an otherwise disconnected graph
Conclusion
In this article, we have gone through a graph traversal technique known as BFS. we have seen the working of BFS and its implementation in different programming languages like C, C++, Java and Python.
We have also seen some of the real-life applications of BFS which clearly shows that BFS is one of the most important algorithms of data structures.