Data Structure and Algorithm
This is an introductory article on algorithms in data structure. In this article, we are going to get a brief overview of algorithms, the role of algorithms in computing and the overview of majorly used algorithms in computer science.
So, let us begin by defining the term ‘Algorithm’.
What is an algorithm?
1. An algorithm is a step-by-step process to solve a particular problem or accomplish a particular task.
2. An algorithm is said to be correct if, for every input, it gives correct/expected output.
3. If the algorithm gives correct output for some inputs and wrong output for certain other inputs, then the algorithm is not correct.
4. We can represent an algorithm in simple English like sentences, as a computer program or as a flowchart.
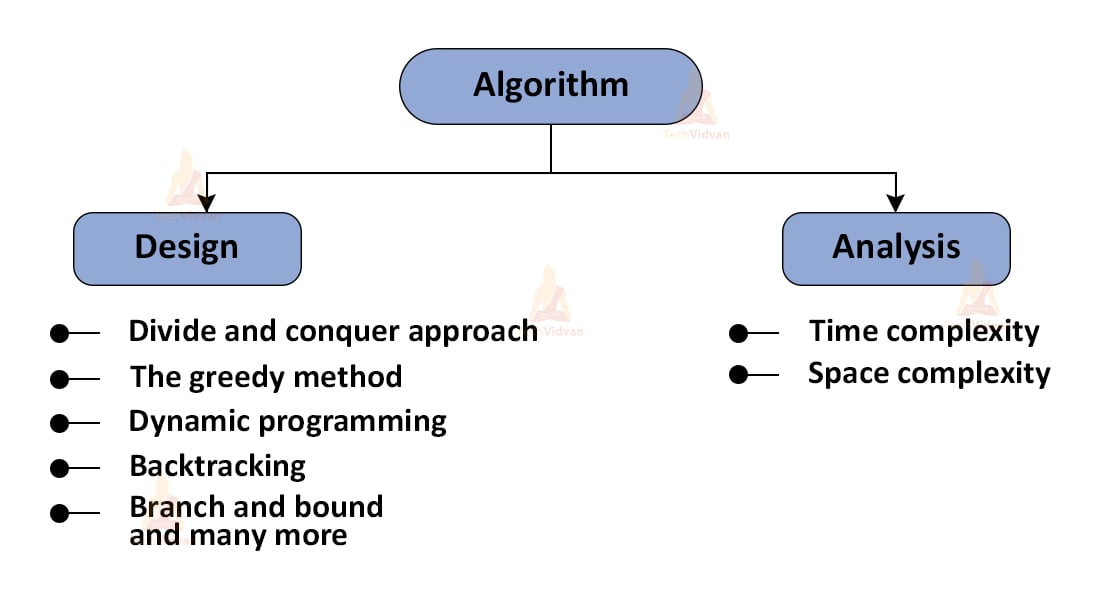
5. Whenever we discuss algorithms in computer science, there are two aspects attached to it:
- Designing an algorithm
- Analyzing an algorithm
Difference between an algorithm and a program:
A program is also a step-by-step procedure to solve a computational problem. However, there is a difference between an algorithm and a program.
| Algorithm | Program |
| An algorithm comprises simple English like steps usually written on paper before we write the program. | A program is the conversion of these simple English like steps into the instruction set in a particular programming language. |
| Algorithms are machine-independent. | A program is machine-dependent. |
| Algorithms are language independent. | Programs are language-dependent. |
| We write the algorithm during the design time. | We write the program during the implementation time. A program is the implementation of the algorithm in a particular programming language. |
Characteristics of algorithm
1. Definiteness
Each instruction is clear and unambiguous. Every step should have only one meaning i.e. no ambiguity.
2. Input
Zero or more well-defined inputs.
3. Output
At least one output is produced. The output must be the same as the expected/desired output.
4. Finiteness
In any case, the algorithm terminates after a finite number of steps.
5. Language independent
An algorithm is never language-specific. We can implement the algorithm in any programming language of our choice.
6. Effectiveness
Every instruction is very basic such that it can be carried out computationally. It is also always feasible.
Dataflow of an algorithm
1. Problem
We first define the problem clearly to design an efficient algorithm for it.
2. Algorithm
It is the set of instructions that aims to solve the above-defined problem.
3. Input
Once we design the algorithm, we input the required values to it for implementation.
4. Processing unit
The input goes to the processing unit which then computes the problem and produces the desired output.
5. Output
It is the final outcome of the algorithm. The algorithm is correctly implemented only if the final outcome is the same as the expected outcome.
Need of an algorithm
There are broadly two reasons why we need algorithms:
1. Scalability
Suppose we have a big real-world problem. To solve such a problem, we first need to break it down into smaller steps i.e. scale down the problem for better analysis and efficiency.
2. Performance
We need to make sure that the solution we want to have for the problem is feasible or not. Designing an algorithm helps to achieve this.
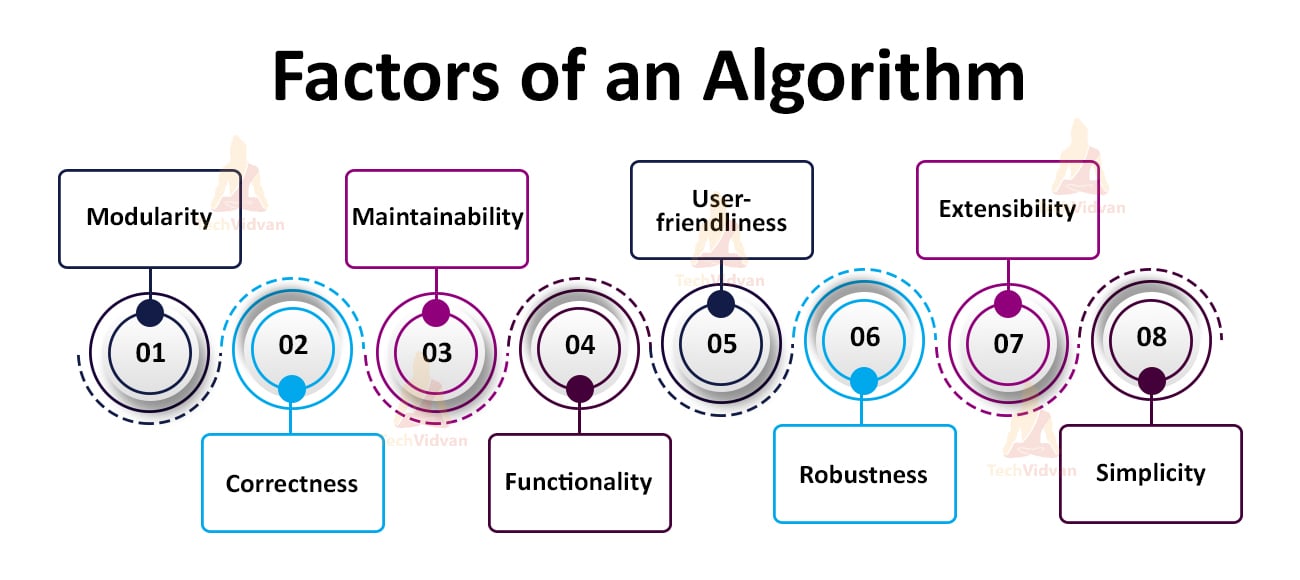
Factors of an algorithm
There are certain factors that we need to take care of while designing an algorithm such as:
1. Modularity
Modularity means breaking the problem into smaller subproblems/modules. A well-designed algorithm is always modular.
2. Correctness
If for a given input, the actual output and the desired output are exactly the same, then the algorithm is correct.
3. Maintainability
It means structuring an algorithm in such a way that it is easily comprehensible. Maintainability also includes being easily able to redefine an algorithm.
4. Functionality
Functionality defines the various logical steps that an algorithm uses to solve computational problems.
5. User-friendliness
An algorithm is user-friendly if the designer is easily able to explain it to the programmer.
6. Robustness
Robustness defines the clarity with which an algorithm can define or solve the problem.
7. Extensibility
An algorithm is extensible if any other designer is also easily able to use it.
8. Simplicity
An algorithm should be simple and easy to understand.
Importance of an algorithm
An algorithm is important from two aspects:
1. Theoretical
If we are not able to understand an algorithm theoretically, then it is very hard to implement it. It is very important to divide a problem into smaller subproblems from a theoretical understanding aspect.
2. Practical
Theory is nothing without implementation. Thus, we are actually able to solve a problem once we implement it.
How to write an algorithm
1. An algorithm is composed of a finite set of steps, each of which requires one or more operations.
2. Although there aren’t any specific rules or well-defined standards on how one should write an algorithm, there is a general layout.
3. Let us try to learn this with the help of a few examples.
Problem statement: Design an algorithm to print ‘TechVidvan’.
Step1: START
Step2: print ‘TechVidvan’
Step3: END
Problem statement: Design an algorithm to input three numbers from the user and print their sum.
Step1: START
Step2: Declare 4 integer variables num1, num2, num3, sum
Step3: Get values of num1, num2, num3
Step4: sum ← num1 + num2 + num3
Step5: Display sum
Step6: END
Problem statement: Design an algorithm to find the factorial of a number
Step1: START
Step2: Declare integer variables num, factorial, i
Step3: Initialize the variables as factorial←1 and i←1
Step4: Input the value of num from the user
Step5: Repeat the following steps until i=n
5.1 factorial ← factorial * i
5.2 i ← i + 1
Step6: print factorial
Step7: END
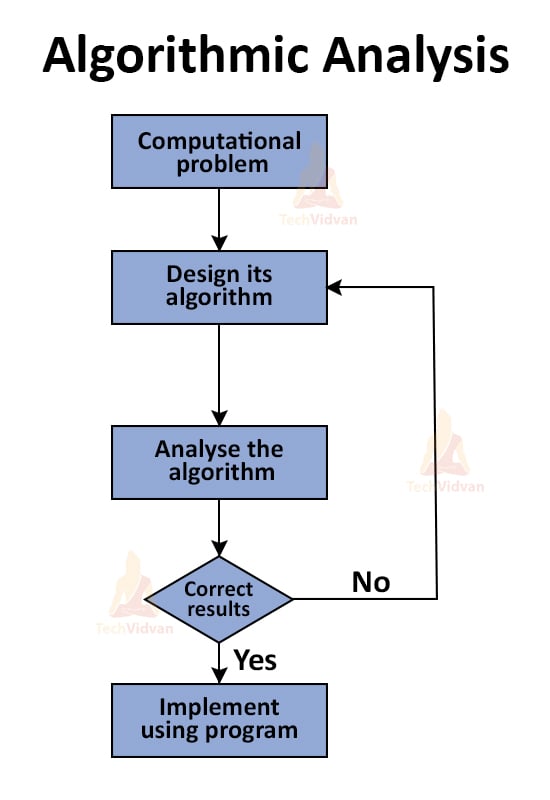
Algorithmic analysis
1. Whenever we encounter a computational problem, we don’t directly start coding it.
2. We first write its algorithm, then analyse the algorithm over different parameters.
3. Once we are sure that the algorithm will get correct results, we implement it in a programming language i.e.
Thus, the efficiency of an algorithm is analyzed at two different stages-
- Before implementation (Prior analysis)
- After implementation (Posterior analysis)
1. Prior Analysis
This analysis is done right after designing the algorithm. The prior analysis is a theoretical analysis where we measure the efficiency of an algorithm by assuming that factors such as processor speed do not affect efficiency.
2. Posterior Analysis
It is the practical analysis of the implemented algorithm. It takes into consideration all the factors such as processor speed, the language in which it is implemented, the hardware involved, etc.
Why analysis?
1. It is possible that for a single problem, there are multiple types of solutions possible i.e. one problem can have multiple algorithms that can solve the problem.
2. For example, if we wish to sort a given sequence of numbers, we can do that using a sorting algorithm.
3. There are multiple types of sorting. In fact, there are almost 150 types of sorting in all.
4. In such a case, we need to decide which algorithm or logic is the best for solving our problem in terms of computation time and space occupied inside the memory.
5. This is where analysis of an algorithm comes into the picture.
Issues of an algorithm
There are majorly two factors that we need to decide through algorithm analysis. These factors are:
1. When can we call an algorithm better than other algorithms for finding the solution to the same problem?
2. What are the criteria of decision/measurement to check which algorithm will perform better?
An algorithm will be better than other algorithms depending upon various criteria for measurement which check the efficiency of any algorithm.
Criteria for measurement of algorithm efficiency
There are two criteria used for the measurement/analysis of the efficiency of any algorithm. These criteria are:
1. Running time of the algorithm
2. Space/memory occupied by the algorithm
Here we are talking about measuring the efficiency of algorithms, not the program.
1. Running time of algorithm
a. The running time of an algorithm means how much time the algorithm will take to execute completely.
b. But, an algorithm is just an abstract representation of a program. It is not the actual implementation.
c. So, how can we find the running time of an algorithm?
d. One way is to actually implement the algorithm into a program and see the time that this program takes for execution. This is the ‘Experimental method’.
e. However, the experimental method has many limitations such as:
i. It is difficult to sit and measure how much time a program takes to execute.
ii. We don’t know the range of input values, which is why we need to manually check for a wide variety of inputs by running the program a lot of times each time with different input. All this is cumbersome.
iii. Whenever programming language comes into the picture, it comes with dependency on the machine. Therefore, depending on the machine’s hardware and the operating system, the running time might vary on two different machines for the same set of code.
iv. If we implement the same algorithm in C and Python, the running times will again vary. C is much faster than Python when it comes to running time. This is because of the presence of bulky modules in Python. Thus, we will get different running times in different programming languages.
f. All these factors conclude that experimental analysis is not a good method to measure the efficiency of any algorithm.
g. We want a generalised method independent of the machine, its hardware, software, programming language as well as capable of working on all possible input sizes.
h. In general, running time will always depend upon input size. Thus, an increase in input size will always increase the running time. This is the basis of our running time analysis.
i. In the whole algorithm analysis, we never measure the accurate running time for any algorithm, rather, we do approximations. We describe it as an asymptotic analysis.
2. Space/Memory
a. This is yet another parameter for analysing any algorithm.
b. The space complexity of any algorithm is the total amount of space/memory occupied by the algorithm concerning the input size.
Let us understand the concept of space complexity using an example. Here, we’ll try to compute the power of a number using two different ways:
i. Using iterative approach
ii. Using recursive approach
and then check out their space complexities.
i. Iterative approach
When we follow the iterative approach to find the power of a number, we make use of local variables. Here, we are using four variables- ‘base’, ‘exponent’, ‘power’, ‘i’ as shown:
int pow_iterative(int base, int exponent)
{
for(i=0; i<exponent; i++)
power = power*base;
}
Here, we just use four auto variables. Thus, the space occupied by this program is of constant order.
ii. Recursive approach
Whenever recursion comes into the picture, stack as well comes along with it because recursion uses the stack for implementation.
While performing recursion, we call the function again and again, which increases the memory used by the program.
The recursive algorithm will be as follows:
{
if(exponent == 1)
return base;
return base * pow_recursive(base, exponent-1);
}
Due to the usage of the stack in recursion, this program has space complexity of the order ‘n’ i.e. linear order which is higher than constant order.
So, we can conclude here that, in terms of space complexity, the iterative approach to find the power of a number is better and more efficient than the recursive approach to computing the same problem.
Algorithmic complexity
By now, we have understood that the performance of an algorithm is measured in two factors- running time, memory used. Based on these two factors, an algorithm has the following two forms of complexity:
1. Time complexity
Time complexity is defined as the amount of time taken by the algorithm for its completion. To calculate the time complexity, we calculate the number of steps an algorithm will take to execute.
2. Space complexity
It is the total memory acquired by the process while executing.
Design of an algorithm
1. There are many ways and approaches to design any algorithm.
2. While designing an algorithm, we must keep in mind the running time of that algorithm and the memory that the algorithm will be using.
3. Thus, during the design of an algorithm, we make use of that approach out of all the possible approaches, which gives the best results in terms of efficiency.
4. We try to minimise the time and space complexity of the algorithm while designing an algorithm for a particular problem.
Approaches of algorithm
There are many standard approaches to design an algorithm based on different strategies. A few of these are:
1. Brute force technique
It is the general and the simplest way to design an algorithm. It simply involves a direct logic-based structure to design an algorithm. This is also called an ‘Exhaustive search algorithm’.
2. Divide and conquer approach
This approach is based on dividing the problem into smaller sub-problems and solving those sub-problems. Once the subproblems are solved, we combine the solutions of those subproblems to get the final solution.
3. Greedy method
This algorithm makes optimal choices at every iteration to get the best possible solution.
4. Dynamic programming
It stores intermediate results to improve the efficiency of the algorithm. It is a recursion-based optimization algorithm. In dynamic programming, we store the results of sub-problems as well so that we don’t need to re-compute even those sub-problems.
5. Randomized algorithm
As the name suggests, this algorithm makes use of random numbers to decide the next step in the algorithm. It involves a certain degree of randomness in its logic. This randomness is involved to reduce the complexity of the algorithm over other standard algorithms.
6. Backtracking
It also solves problems recursively. It involves searching every possible combination for solving a computational problem and removing those sub-solutions that don’t satisfy the constraints of the problem.
7. Branch and bound
It is an optimization algorithm used to solve combinatory, discrete and general mathematical problems. It involves dividing the problem, obtaining sub-solutions for them and then finding the most optimal solution.
Techniques used for designing different algorithms are also termed algorithm design patterns.
Designing the technique of an algorithm plays a very important role in the computation process as it will decide the computation time and memory occupied by the algorithm.
Categories of algorithms
1. Search
Algorithm used to search for a particular item in a data structure.
2. Sort
Algorithm to sort the elements in a particular order.
3. Delete
Algorithm used to delete a particular element from a data structure.
4. Insert
Algorithm to insert a particular item in a data structure.
5. Update
Algorithm used for updating the existing elements in a data structure.
Types of algorithms
There are majorly two types of algorithms: searching algorithms and sorting algorithms.
1. Searching algorithm
a. To search for a particular memory location or a particular value out of a huge chunk of data present inside the computer memory, we use searching algorithm techniques.
b. There are various types of search techniques such as linear search, binary search, etc.
2. Sorting algorithm
a. Sorting techniques are used in data structures to rearrange the values in a particular order.
b. The order could be increasing, decreasing, non-increasing, non-decreasing, etc.
Need for sorting algorithms
a. For optimizing the efficiency of other algorithms such as binary search.
b. For producing information in a sorted order as it is more readable.
c. Searching a particular element in a sorted list is easier than in an unsorted list.
Conclusion
This article gives an overview of what an algorithm is in computer science and its importance in the computation process. Any good programmer will first design and analyze the software before implementing it. This is why writing algorithms before implementing solutions to a particular problem is a preferred approach. This makes algorithms very important from the aspect of solving computational problems.
In the next article, we will study asymptotic analysis and how exactly we measure the complexities of any algorithm.