Doubly Linked List in Data Structure
Linked lists are a widely used data structure because of their wide range of applications. Linked lists are also of three types:
1. Singly linked list
2. Doubly linked list
3. Circular linked list
This article will cover doubly linked list in detail.
What is a doubly-linked list?
The singly linked list had a single pointer pointing to the next node. But a doubly linked list contains two pointers. One pointer points to the next node and one pointer to the previous node. Thus, a doubly linked list is a two-way chain.
Every node in a doubly linked list has-
- Data
- Address of the next node
- Address of the previous node
The purpose of a doubly linked list is to enable both-way traversal while still allowing non-contiguous memory storage. Just like a singly linked list, we need to have a starting pointer pointing to the first node. The last node in the list points to NULL.
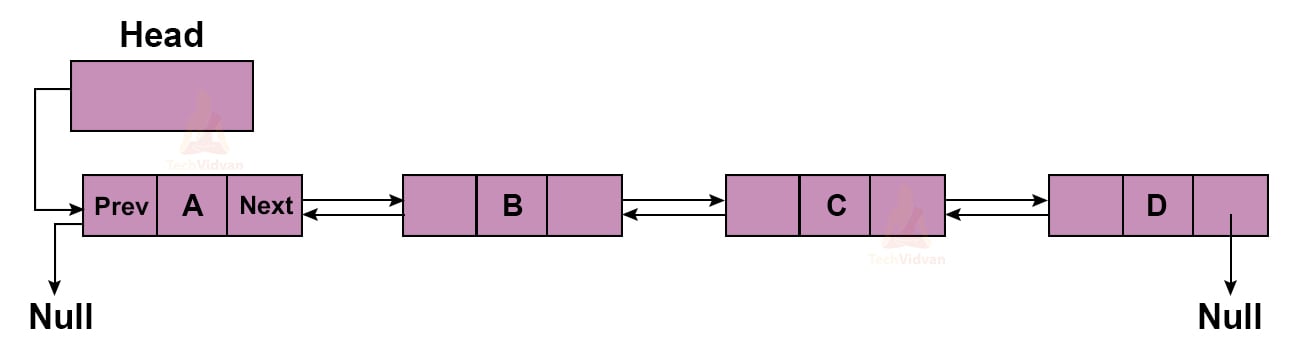
Representation of Doubly Linked List
A doubly linked list is represented as follows:
The above list is comprised of 4 nodes having four data points- A, B, C, D. Each node has two links one pointing forward and one pointing backwards.
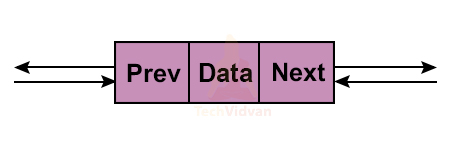
Each node has the following structure:
It comprises of two pointers and a data field.
a. Data: It constitutes the value of the data item inside the list.
b. Prev: It is a pointer pointing towards the previous node. For the first node, Prev points to NULL.
c. Next: It links the current node to the next node in the linked list. The ‘Next’ of the last node points towards NULL.
Basic Operations on Double Linked List
The basic set of operations that we can perform on a doubly linked list are:
1. Traverse forward: It means visiting each node from the beginning till the end with the help of the ‘Next’ pointer.
2. Traverse backwards: This operation is performed to visit each node but in the reverse direction. It will traverse the list from the end to the beginning.
3. Insertion: This operation inserts an element at any given position in the list.
4. Deletion: Deletion operation helps in deleting a node from the linked list.
5. Display forward: This operation is used to print/display all the data elements of the linked list from beginning till the end.
6. Display backwards: it will display the elements from the end to the beginning.
7. Search: Search operation helps in searching an element by traversing it.
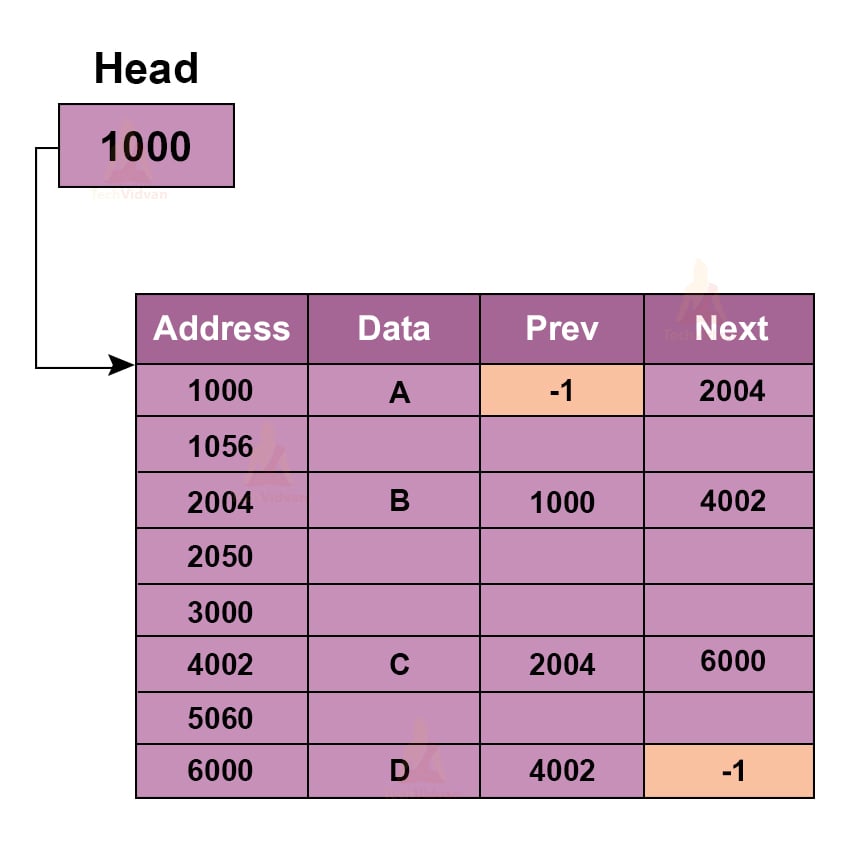
Memory Representation of Doubly Linked List
1. Each node in a doubly-linked list consists of 3 parts- two-pointers and a node.
2. Due to two-pointers additional to data values, a doubly-linked list takes a lot of space as compared to other data structures.
3. The following image shows the memory representation of a linked list.
4. Here, -1 represents NULL.
5. The Prev of the first node i.e. A and the Next of the last node i.e. D point towards NULL.
6. This memory representation shows that the values need not be stored contiguously.
7. The values 1000, 1056, 2004 and so on represent addresses in the memory.
8. We traverse the list until we find -1 in the Next of a node.
Creating a Node in Doubly Linked List
Each node in a doubly linked list has data as well pointers. Therefore, we use a structure to create the node.
The structure template for the node looks as follows:
struct Node
{
int data; //The data point
struct Node *Prev; //Pointer to the previous node
struct Node *Next; //Pointer to the next node
};
Traversal in a Doubly Linked List
Traversal refers to linearly visiting each node. In a doubly linked list, we can traverse in both forward and backward directions.
The function to perform the traversal is as follows:
List_traversal(struct Node *Head)
{
Prev = (struct Node *)malloc(sizeof(struct Node));
Next = (struct Node *)malloc(sizeof(struct Node));
if(Head == NULL) //If the list is empty
return;
while(Next->data != NULL)
{
Print(Next->data); //The display operation
Next = Next->data;
}
}
The time complexity for the traversal operation is O(n).
Doubly Linked List Methods
There are various inbuilt methods defined inside the doubly-linked list class. A few of these methods are:
1. add_front: This method adds a new node at the beginning of the doubly linked list.
2. add_after: It adds a new node after a particular node.
3. add_before: It is used to add a new node before a particular node in the list.
4. add_end: This method will add a new node at the end of the doubly linked list.
5. forward_traverse: It helps in traversing the list in the forward direction.
6. backward_traverse: It helps in traversing the list in the backward direction.
7. delete: This method deletes a node from the linked list.
Their implementation inside the class is shown below:
class doubly_linked_list
{
node *First; // It points to the first node of the list
node *Last; // It points to the last node of the list
public:
Doubly_Linked_List()
{
front = NULL;
end = NULL;
}
void add_front(int ); //Adds a new node at the beginning
void add_after(node* , int ); //Adds a new node after the given node
void add_before(node* , int ); //Adds a new node before a given node
void add_end(int ); //Adds a new node at the end of the list
void delete_node(node*); //Ddeletes a particular node
void forward_traverse(); //traverses the doubly-linked list in forward direction
void backward_traverse(); //traverses the doubly-linked list in backward direction
};
Insertion in a Linked List
Insertion in a linked list occurs at three different positions:
1. Insertion at the beginning of the list
2. Insertion after a particular node.
3. Insertion at the end of the list
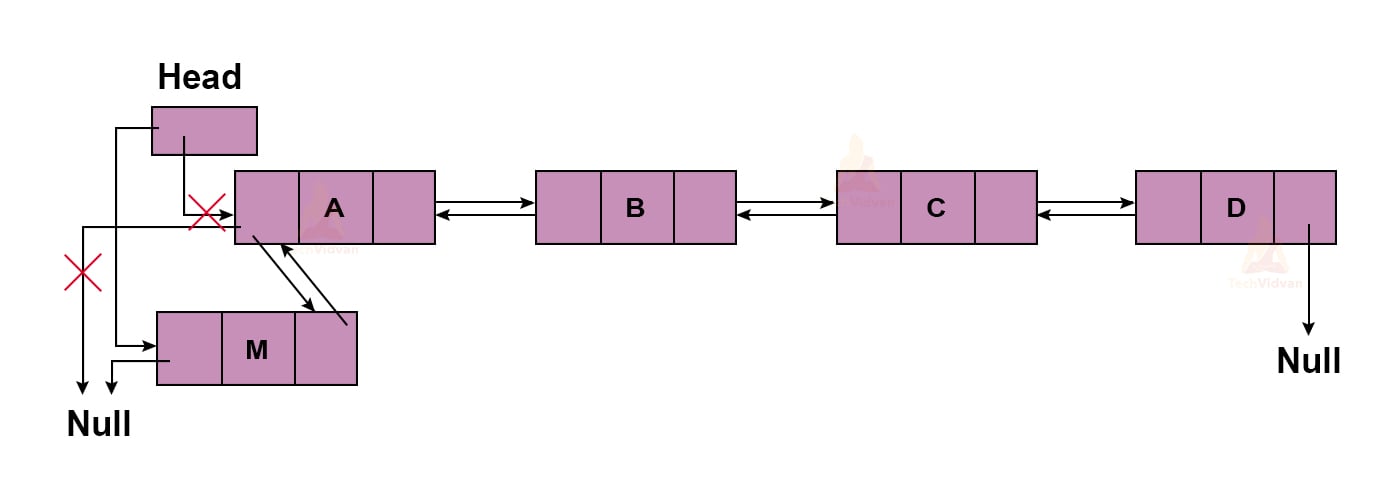
Insertion at the beginning
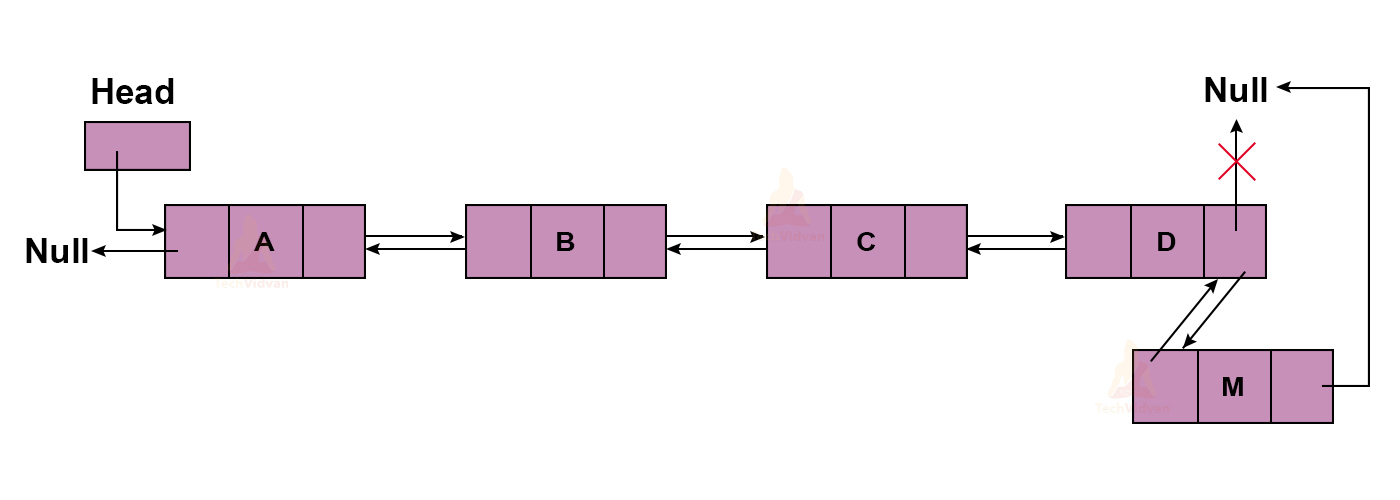
We insert a node at the beginning such that the next pointer points to the node which was at first before. The previous pointer points to NULL.
Here, we have tried to insert M at the beginning.
The pseudo-code for this operation will be:
Insertion_at_beginning(struct Node *Head, int key)
{
Prev = (struct Node *)malloc(sizeof(struct Node));
Next = (struct Node *)malloc(sizeof(struct Node));
temp = (struct Node *)malloc(sizeof(struct Node));
if(Head == NULL)
return;
while(Next->data != NULL)
{
temp->data = key;
temp->Next = Head;
Head->Prev = temp;
Head = temp;
temp->Prev = NULL;
}
}
Here, we will make use of an extra pointer ‘temp’ to perform the insertion operation.
Insertion at the End
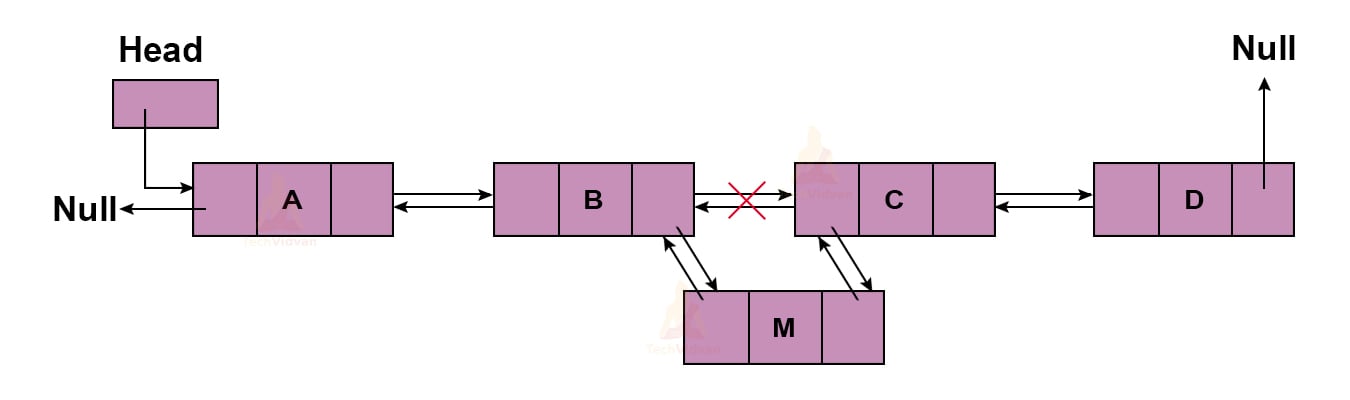
If the list is empty, we will insert a node right after the Head. If the list is not empty, we first need to traverse the whole list to insert a node at the end of the list.
In the above diagram, we are inserting M at the end.
The function for insertion at the end is:
Insertion_at_end(struct Node *Head, int key)
{
Ptr = (struct Node *) malloc(sizeof(struct node));
Ptr->Next = NULL;
Ptr->Prev=NULL;
Ptr->data = key;
Head = Ptr;
Temp = head;
while (temp != NULL)
temp = temp -> next;
temp->Next = Ptr;
Ptr->Prev = temp;
Ptr->Next = NULL;
}
Insertion after a particular node
Insertion after a particular node involves traversing all nodes before that node. We will make use of an extra pointer ‘temp’ for traversing the node up to a particular position.
For example, suppose we wish to insert a node having data value ‘M’ between node ‘B’ and node ‘C’, we will do it as follows:
The function will be:
Insert_after_particular_position(struct Node *Head, int key)
{
Ptr = (struct Node *) malloc(sizeof(struct node)); //Allocating memory for the new node
temp = Head;
Ptr->data = key;
for(i=0; i<position; i++)
{
temp = temp->Next;
if(temp == NULL) // i.e. if the list is empty
return;
}
Ptr->Next = temp->Next;
Ptr->Prev = temp;
temp->Next = Ptr;
temp->Next->Prev = Ptr;
}
Time complexity of Insertion:
| Insertion operation | Complexity |
| At the beginning | O(1) |
| After a particular node | O(1) |
| At the end | O(n) |
Deletion from a Linked List:
Deletion involves deleting nodes from the list. It also works in three different cases:
1. Deletion from beginning
2. Deletion at the end
3. Deleting a node other than the first and the last node
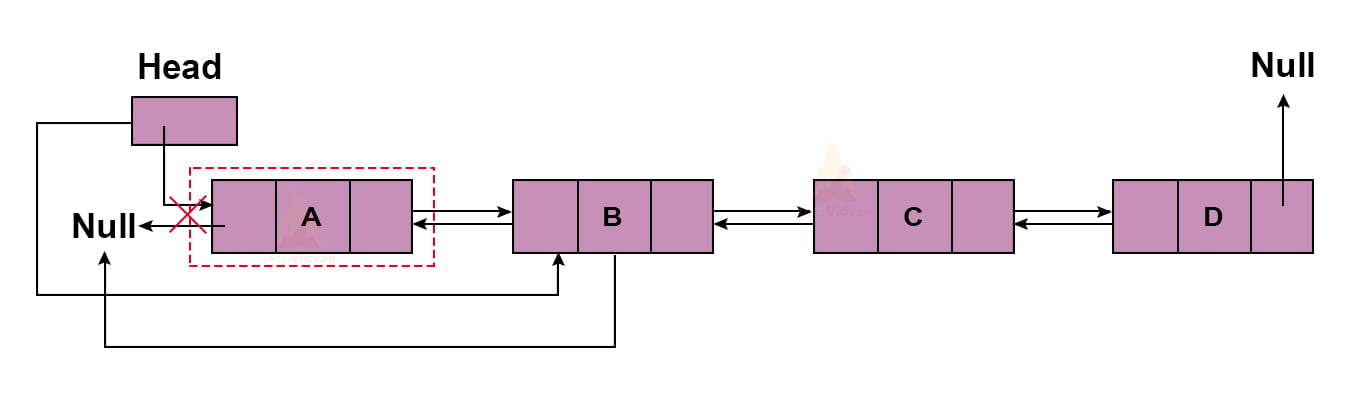
1. Deletion from the beginning:
It involves deleting the first node of the doubly linked list. The following diagram shows the deletion operation at the beginning of the doubly linked list.
The deletion function will be:
Deletion_from_beginning(int key){
struct Node *Ptr = Head;
if (Head == NULL) return;
Head = Head->Next;
Head->Prev = NULL;
free(Ptr);
}
The free function is used to release the memory space. If we don’t release memory after using it, it might lead to memory leakage problems in future.
2. Deletion at the end:
If the list is empty, we will directly pass the return statement in the function. If the list contains a single node, we just need to make the Head point towards NULL. When the list has two or more nodes, we need to traverse the whole node and then delete the last node.
Deletion_at_end(int key){
struct Node *Ptr = Head;
if(Head == NULL) //If the list is empty
return;
if(Ptr->Next == NULL) //If the list has only one element
{
Head->Next = NULL;
return;
}
Ptr->Prev->Next = NULL;
free(ptr);
}
Deletion after a particular node:
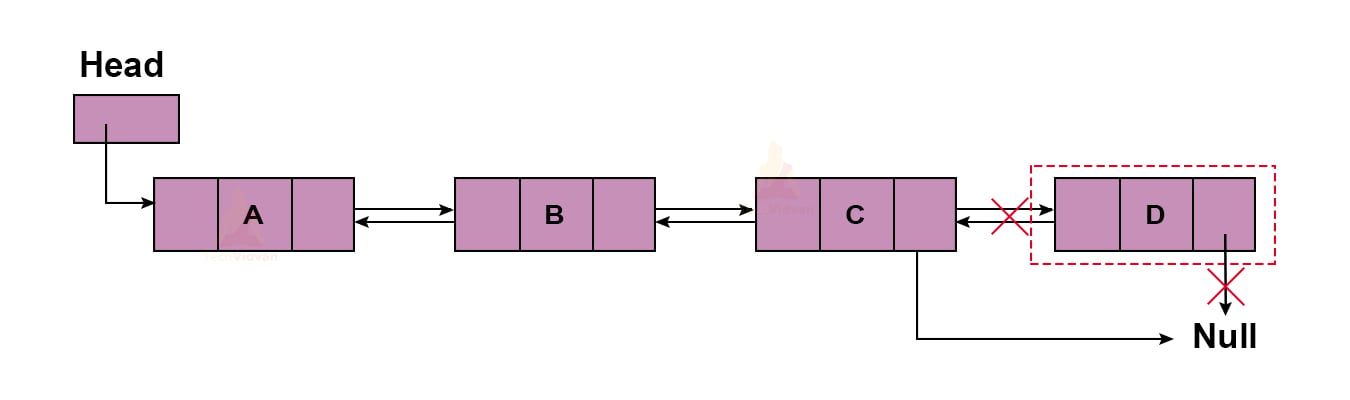
If we know the address of a particular node, we can easily delete the node next to it.
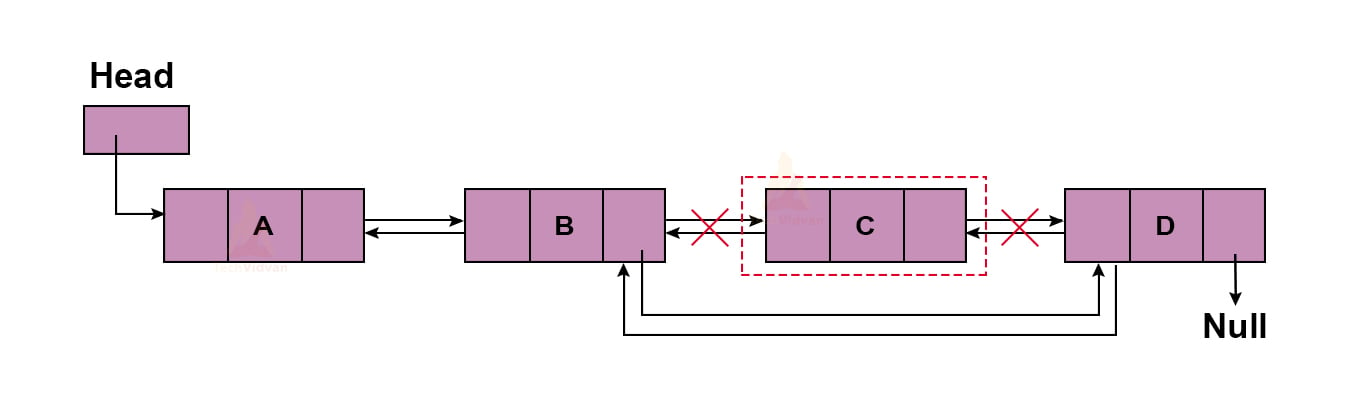
For example, suppose we wish to delete node ‘C’ from the list having nodes: ‘A’, ‘B’, ‘C’ and ‘D’. Then, we will do it as follows:
The function will be:
Deletion_after_particular_node(int key){
struct Node *temp = Head;
if(Head == NULL) //If the list is empty
return;
if(temp -> Next == NULL) //If the list has only 1 node
return;
while(temp->data != key) //Traversing the list
temp = temp->Next;
if(temp->Next->Next == NULL) //If the node to be deleted is the last node
temp->Next = NULL;
Ptr = temp->Next;
temp->Next = Ptr->Next;
Ptr->Next->Prev = temp;
free(ptr);
}
Time complexity for Deletion operation:
| Deletion operation | Complexity |
| At the beginning | O(1) |
| After a particular node | O(n) |
| At the end | O(n) |
Doubly Linked List as Circular Linked list:
A doubly linked list contains pointers to both the previous and the next node. A circular list does not contain any NULL pointer. In a circular linked list, the ‘Next’ of the last nodes points to the first node of the list.
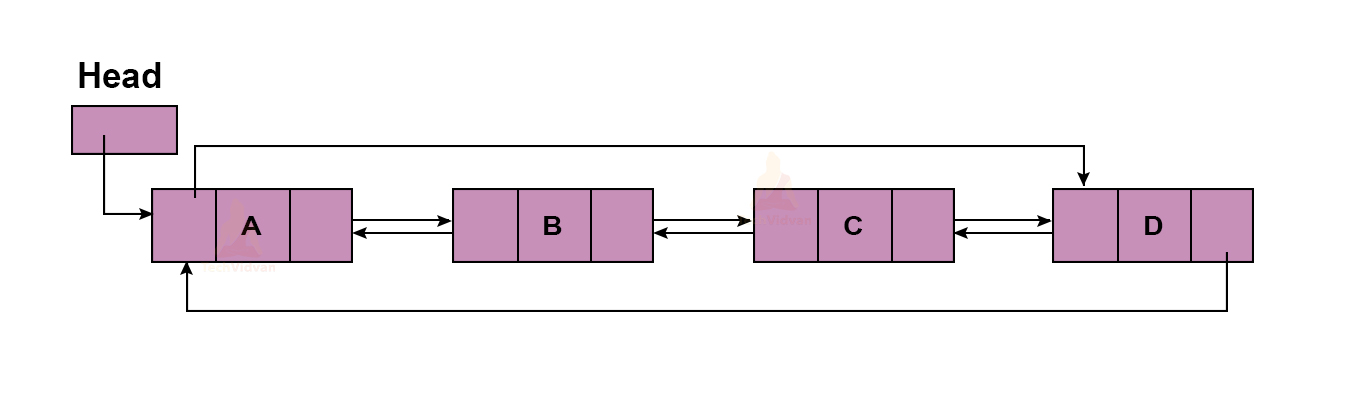
Combination of a doubly list and a circular list is known as a doubly-circular list. A doubly-circular linked list looks as follows:
1. The ‘Next’ pointer of the last node in the doubly-linked list points to the points to the first node in the list.
2. The ‘Prev’ pointer of the first node points to the last node of the linked list.
3. There is no NULL pointer anywhere in the list.
Advantages of a Doubly Linked List:
1. We can traverse a doubly linked list in both forward and backward direction.
2. Traversal in the backward direction makes the deletion operation more efficient. If the pointer to a node is given, we can easily delete the previous node with O’s time complexity O(1).
3. The insertion operation is also more efficient. If the pointer a node is given, we can easily insert a node before that node.
Disadvantages of a Doubly Linked List:
1. A doubly linked list takes more space than a singly list because of the presence of an extra ‘Prev’ pointer at each node.
2. We need to maintain this extra ‘Prev’ pointer while performing all the operations. This increases the space complexity of all the operations performed on a doubly linked list.
Conclusion
The crux of this article is that a doubly linked list has a similar behaviour as a singly list most of the time. However, there are a few cases when a double list performs better than a singly linked list. Insertion and deletion operations are easier and more efficient in a doubly-linked list as compared to a singly linked list. But they are easier at the cost of additional space for the program.