Graphs in Data Structure
In this article, we will learn about the graphs in data structure.
There are mainly 2 types of data structures: Linear and Non-linear. Linear data structures include arrays, linked lists, stacks, queues, etc. whereas the non-linear data structures include trees and graphs.
Thus, a graph is a non-linear data structure and it consists of edges and vertices. Graphs are one of the most important topics of data structures.
What are Graphs in data structure?
A graph is a collection of two sets:
1. A set of vertices, and
2. A set of edges
We can represent every edge by two elements of the set. A graph is represented by G(V, E) where V= set of vertices and E= set of edges. Vertices are also known as nodes.
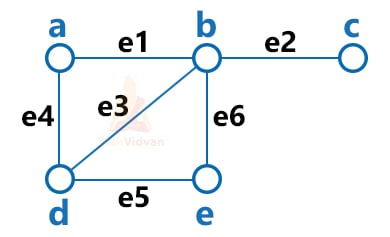
For example, the following diagram depicts a graph:
Here, V = {a, b, c, d, e} and E = {e1, e2, e3, e4, e5, e6} or E = {ab, bc, bd, ad, de, ce}.
Graphs in data structure
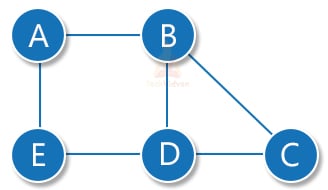
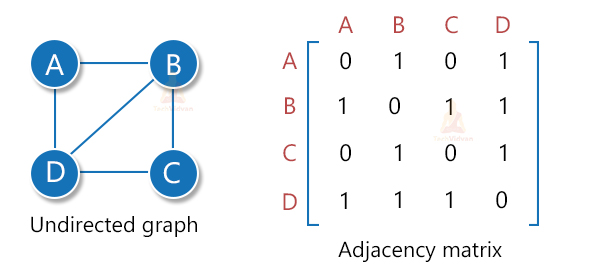
1. Undirected graph: An undirected graph is the one in which there is no direction associated with the edges. In an undirected graph, traversal from A→B is the same as that of B→A. the following graph is undirected:
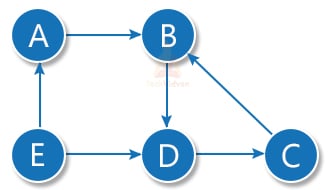
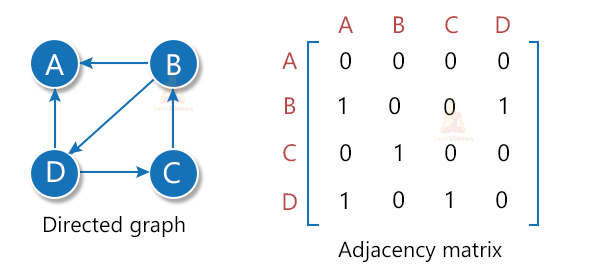
2. Directed graph: a directed graph is the one in which we have ordered pairs and the direction matters. Thus, in a directed graph, A→B is not the same as B→A. The following graph is a directed graph.
Here, the edge is from A to B. Thus, A is called the initial node and B is called the terminal node.
Graph Terminologies:
Consider the following graph:
1. Vertex: A vertex represents each node of a graph. For example, in the above graph, A, B, C, D, E are the vertices.
2. Edge: It is the path between two nodes/vertices.
3. Path: It is the sequence/order of vertices to reach from one node to another. For example, suppose we wish to reach from node A to node E. the possible paths are: A→C→E or A→B→C→E.
4. Closed path: If the initial and the final nodes are the same, then the path is a closed path.
5. Simple path: A simple path is a path in which all the nodes are distinct.
6. Adjacency: Two vertices are adjacent if there exists an edge that connects those two vertices. For example, the nodes A-B, B-C, A-C, C-D, C-E are all adjacent nodes.
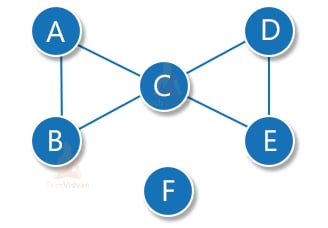
7. Degree of a node: For each node in a graph, its degree is the number of edges connected to that node. Here, the degree of all nodes except node F is 2 and the degree of node F is 0.
8. Isolated node: A node having degree = 0. Thus, an isolated node is not connected to any other node. Here, node F is the isolated node.
Types of Graphs:
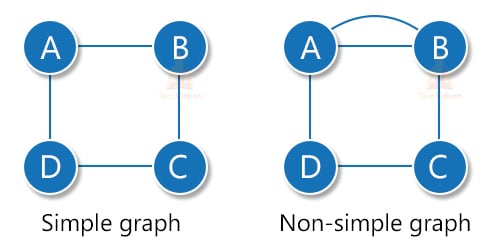
1. Simple graph: A graph in which neither loops nor parallel edges exist is a simple graph. The following diagram is an example of a simple graph.
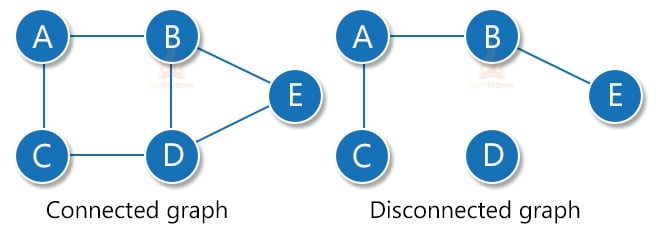
2. Connected graph: If there is a path between every pair of vertices, then the graph is called a connected graph. Any graph containing an isolated edge can never be a connected graph. The first graph In the following example is connected whereas the second one is not a connected graph.
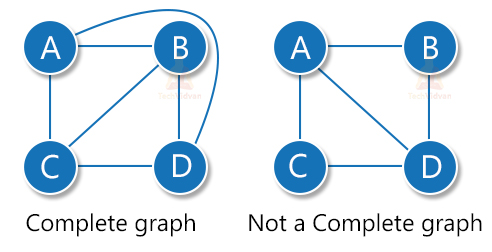
3. Complete graph: A complete graph is a simple graph in which every node is adjacent to every other node. A complete graph has nC2 = n(n-1)/2 edges.
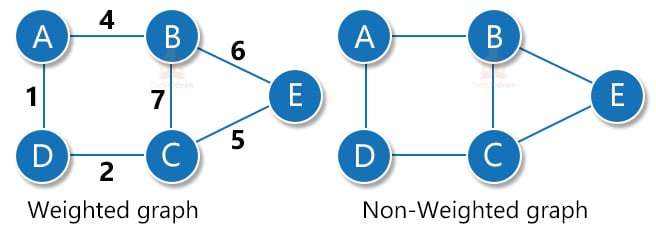
4. Weighted graph: A weighted graph is the one in which we associate some weight with every edge. For example, the following graph is a weighted graph:
5. Digraph: It is a kind of directed graph in which each edge of the graph has a specified direction and we can traverse through the graph only in that direction.
Graphs Representation in data structure:
The complexity of any graph-based algorithm depends upon how we are implementing the graphs. That is why the graph representation becomes important.
There are many ways to represent graphs. However, two of them are most popular: Adjacency matrix representation and linked list representation
1. Adjacency matrix representation
In adjacency matrix representation, we have a matrix of order n*n where n is the number of nodes in the graph. The matrix represents the mapping between various edges and vertices.
In the matrix, each row and column represents a vertex. The values determine the presence of edges.
Let Aij represents each element of the adjacency matrix. Then,
For an undirected graph, the value of Aij is 1 if there exists an edge between i and j. Otherwise, the value of Aij is 0.
For a directed graph, the value of Aij is 1 only if there is an edge from i to j i.e. i is the initial node and j is the terminal node.
The time complexity of the adjacency matrix is O(n2).
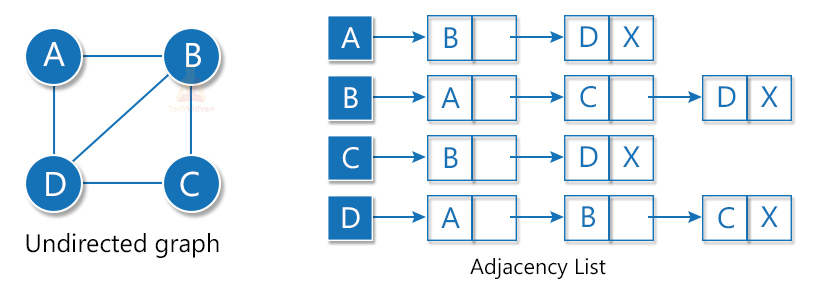
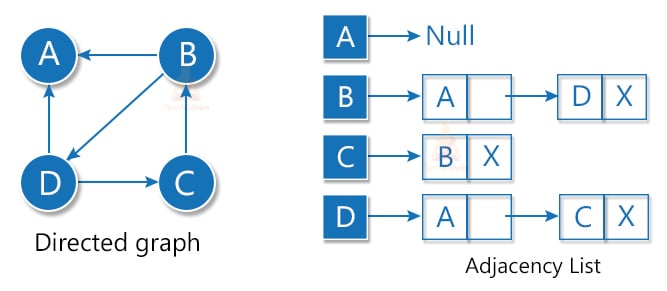
2. Adjacency list representation
The adjacency list is an array of linked lists where the array denotes the total vertices and each linked list denotes the vertices connected to a particular node.
In a linked list, the most important component is the pointer named ‘Head’ because this single pointer maintains the whole linked list. For linked list representation, we will have total pointers equal to the number of nodes in the graph.
For an undirected graph, we will link all the edges in the list that are connected to a node as shown:
In a directed graph, we will link only the initial nodes in the list as shown:
Adjacency Matrix Implementation in C:
#include <stdio.h>
#define S 4
void init(int Array[][S])
{
int i, j;
for (i = 0; i < S; i++)
for (j = 0; j < S; j++)
Array[i][j] = 0;
}
void addEdge(int Array[][S], int i, int j)
{
Array[i][j] = 1;
Array[j][i] = 1;
}
int main()
{
int adjacency_matrix[S][S];
init(adjacency_matrix);
addEdge(adjacency_matrix, 1, 2);
addEdge(adjacency_matrix, 0, 2);
addEdge(adjacency_matrix, 3, 0);
addEdge(adjacency_matrix, 2, 3);
int i, j;
for (i = 0; i < S; i++)
{
printf("%d: ", i);
for (j = 0; j < S; j++)
printf("%d ", adjacency_matrix[i][j]);
printf("\n");
}
return 0;
}
Adjacency Matrix Implementation in C++
#include <bits/stdc++.h>
using namespace std;
#define S 4
void init(int Array[][S])
{
int i, j;
for (i = 0; i < S; i++)
for (j = 0; j < S; j++)
Array[i][j] = 0;
}
void addEdge(int Array[][S], int i, int j)
{
Array[i][j] = 1;
Array[j][i] = 1;
}
int main()
{
int adjacency_matrix[S][S];
init(adjacency_matrix);
addEdge(adjacency_matrix, 1, 2);
addEdge(adjacency_matrix, 0, 2);
addEdge(adjacency_matrix, 3, 0);
addEdge(adjacency_matrix, 2, 3);
int i, j;
for (i = 0; i < S; i++)
{
cout << i << ":";
for (j = 0; j < S; j++)
cout << " " <<adjacency_matrix[i][j];
cout << "\n";
}
return 0;
}
Implementation of Adjacency Matrix in Java:
public class DS_Graph
{
private boolean adjacent_matrix[][];
private int Vertices;
public DS_Graph(int Vertices)
{
this.Vertices = Vertices;
adjacent_matrix = new boolean[Vertices][Vertices];
}
public void addEdge(int i, int j)
{
adjacent_matrix[i][j] = true;
adjacent_matrix[j][i] = true;
}
public void deleteEdge(int i, int j)
{
adjacent_matrix[i][j] = false;
adjacent_matrix[j][i] = false;
}
public String toString()
{
StringBuilder s = new StringBuilder();
for (int i = 0; i < Vertices; i++)
{
s.append(i + ": ");
for (boolean j : adjacent_matrix[i])
{
s.append((j ? 1 : 0) + " ");
}
s.append("\n");
}
return s.toString();
}
public static void main(String args[])
{
DS_Graph g = new DS_Graph(4);
g.addEdge(1, 2);
g.addEdge(0, 2);
g.addEdge(3, 0);
g.addEdge(2, 3);
System.out.print(g.toString());
}
}
Adjacency Matrix Implementation in Python:
class DS_Graph(object):
def __init__(self, size):
self.adjacent_matrix = []
for i in range(size):
self.adjacent_matrix.append([0 for i in range(size)])
self.size = size
def addEdge(self, x, y):
self.adjacent_matrix[x][y] = 1
self.adjacent_matrix[x][y] = 1
def deleteEdge(self, v1, v2):
self.adjacent_matrix[x][y] = 0
self.adjacent_matrix[x][y] = 0
def __len__(self):
return self.size
def Dispay_matrix(self):
for row in self.adjacent_matrix:
for val in row:
print('{:4}'.format(val), end="")
print()
if __name__ == '__main__':
g = DS_Graph(5)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(3, 0)
g.addEdge(2, 3)
g.Dispay_matrix()
Advantages of Adjacency Matrix:
- Performing operations on a matrix are easier as compared to performing them on the list or other data structure. Operations like adding and removing edges, checking if the edges are present in the graph or not are easily performable.
- We can perform heavy matrix operations easily on modern GPUs.
- Using the adjacency matrix method proves to be very efficient whenever the graph is dense and when the number of edges present in the graph is large.
Disadvantages of Adjacency Matrix:
- In the adjacency matrix method, operations such as inEdges and outEdges are costly.
- Matrix representation requires a large amount of additional memory even if the number of edges in a graph is less. This sometimes leads to a huge wastage of memory.
Operations performed on Graphs in Data Structures:
The most common operations on a graph are:
1. Graph traversal: It includes traversing all the edges of a graph.
2. Display vertex: It helps to display one or more vertices of the graph.
3. Add vertex: This operation adds a new vertex to the graph.
4. Add edge: It helps to add an edge between a given pair of vertices.
5. Checking if the element is present in the graph or not.
6. Finding the path from one edge to another.
Practical Applications of Graph:
1. Facebook connections: Almost every one of us uses Facebook for connecting with friends. Everything is a node on Facebook. Thus, our profile and our friends’ profiles are also nodes. All of them are interconnected. Facebook makes use of graphs to give us friend suggestions.
2. WWW: World Wide Web is the biggest graph. All the links and hyperlinks are the nodes and their interconnection is the edges. This is why we can open one webpage from the other.
3. Google maps: Google maps is also based on graphs. All the cities/towns/places are the nodes and we have different paths between different places.
Conclusion:
Looking at the wide variety of applications that graphs in data structure offer, we can say that graphs are one of the most important topics in computer science.
Without graphs, there would have been no fast searching, no connecting with friends on the internet and no locating of places through online applications.
In this article, we have gone through the definition of graphs, their types, their representation methods and the operations performed on the graphs.