TechVidvan

Heap Sort – Algorithm, Working and Implementation

Heap sort is a sorting technique based upon heap data structure. It makes use of a binary heap for sorting the elements. Heapsort is a comparison-based sorting algorithm. It is an inplace sorting technique. Heapsort is not a stable algorithm.

To implement heapsort, we make use of either min-heap or max-heap. We create a min-heap or a max-heap out of the given array elements and the root node is either the minimum or the maximum element respectively. In every iteration, we delete the root node and store it in the sorted array. Thus, the heapsort algorithm is somewhat similar to the selection sort. In selection sort as well, we used to select the minimum element and insert it into the sorted array.

Heapsort involves mainly two steps to be performed:

1. Building a max-heap or min-heap using the elements of the given array.
2. Deleting the root node of the heap formed in every iteration.

What is a Binary Heap?

A binary heap is a complete binary tree. This means that every node can have at most two elements and the elements are filled in the nodes from left to right. In a complete binary tree, we cannot move to the next node for inserting elements until the previous node is full in its capacity.

A binary heap can be of two types:

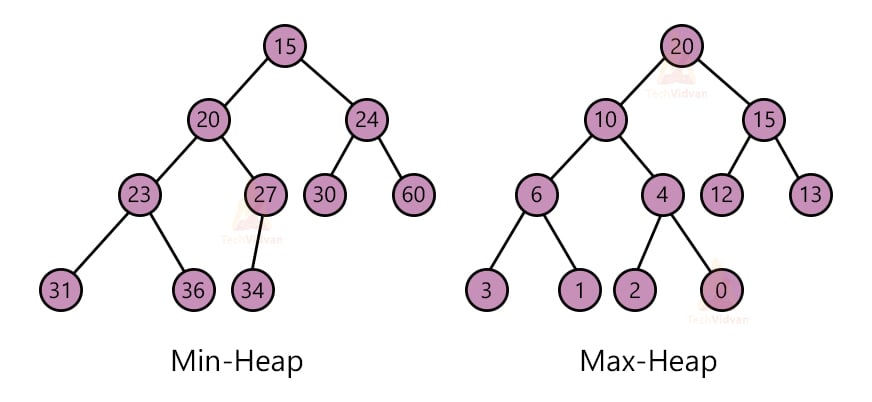
1. Min-heap: In a min-heap, the value of the parent node is smaller than both of its children nodes.

2. Max-heap: In a max-heap, the value of the parent node is greater than both of its children nodes.

The following diagram shows a min-heap and a max-heap respectively.

Max Min Heap

Why Array-based Representation for Binary Heap:

Array-based representation is the best for binary heap because of the following factors:

  • Array-based representation is space-efficient.
  • Heap is a complete binary tree. Hence, it is easier to represent it in the form of an array.
  • If we know the index/position of the parent node, we can easily find the position of its left and right child. If the array starts from index 0 and the parent node is at an index ‘i’, then its left child will be at the position 2*i + 1. Its right child will be at the position 2*i + 2.

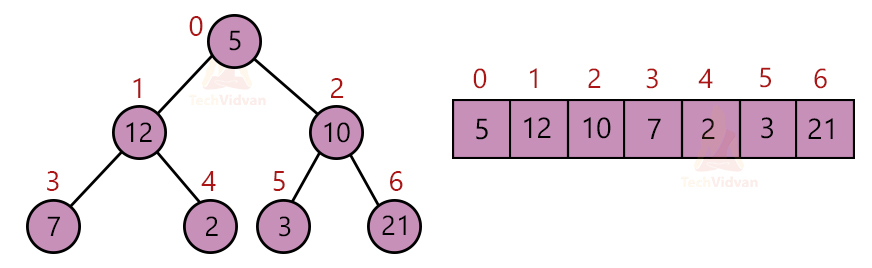
Relationship between Array indices and Tree elements:

In a complete binary tree, we can easily access the left and the right child of a particular parent node using a fixed set of formulae. If the index starts from 0 and the parent node is at an index ‘i’, then its left child will be at the position 2*i + 1. Its right child will be at the position 2*i + 2. We can also find the parent of any node if we know the index of the child. If the index of a child node is ‘i’, then its parent will be at the index (i-1)/2.

 

Heap sort in D

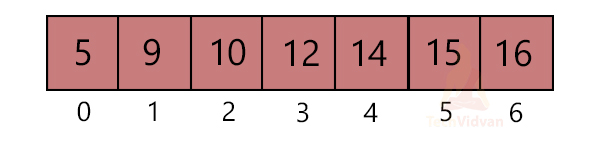
Example:
Let us try to find out the left and the right child of 10. 10 is at position 2 in the heap.
The left child of 10 = Index(2*i + 1) = Index(2*2+1) = Index(5) = 3
The right child of 10 = Index(2*i +2) = Index(2*2+2) = Index(6) = 21

Similarly, let’s try to find the parent of 3 whose index is 5 in the array.
The parent of 3 = Index((i-1)/2) = Index((5-1)/2) = Index(2) = 10

Heapify:

The procedure to convert a simple binary heap into a min-heap or a max-heap is defined as the Heapify process.

Procedure for Heapify:

The function to perform the heapify operation for a max-heap is as follows:

Heapify(array[], n, i):
    largest = i;
    left = 2 * i + 1;
    right = 2 * i + 2;
    if (left < n) and (array[left] > array[largest]):
            largest = left;
    if (right < n) and (array[right] > array[largest]):
        largest = right;

    if (largest != i):
        swap(array[i], array[largest]);
        Heapify(array, n, largest);
    END if
END Heapify

Working of Heap Sort:

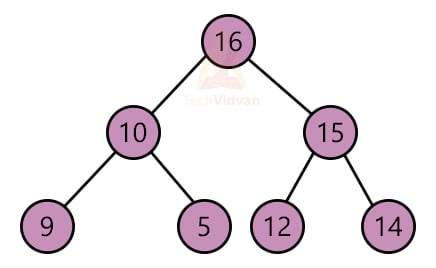
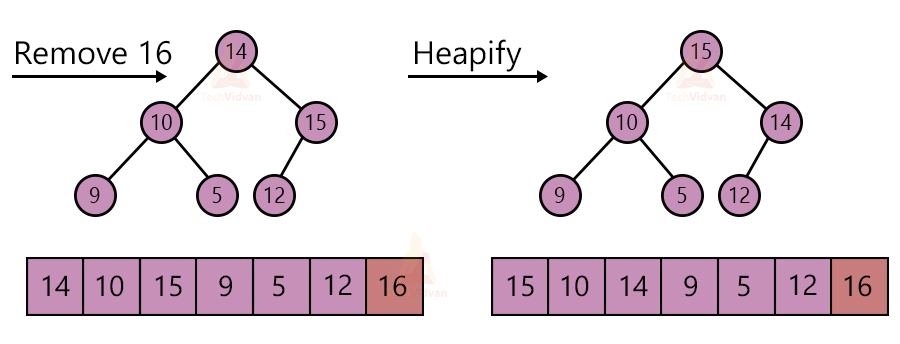
Consider an array having elements: 16, 10, 15, 9, 5, 12, 14.
Suppose that they are arranged in a tree following the max-heap property as shown:

Heap sort in DS

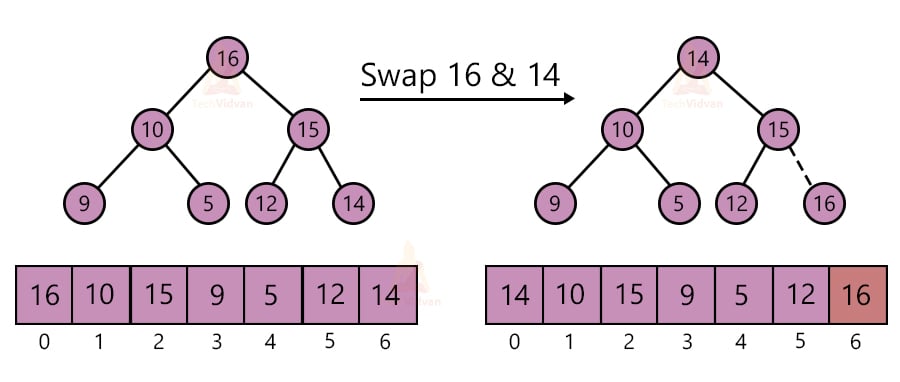
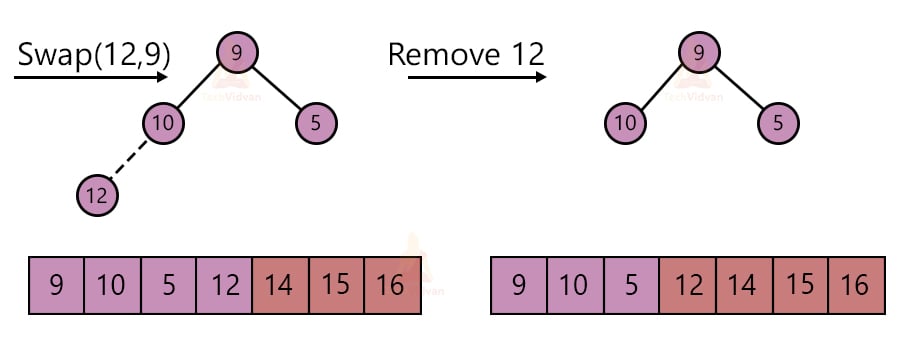
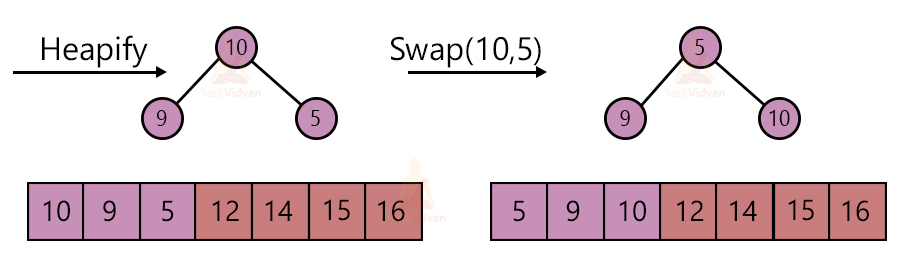
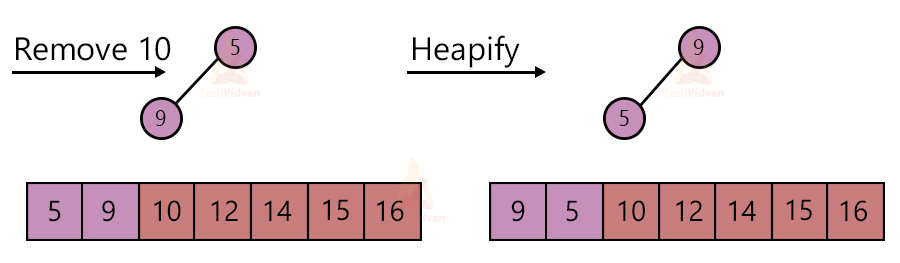
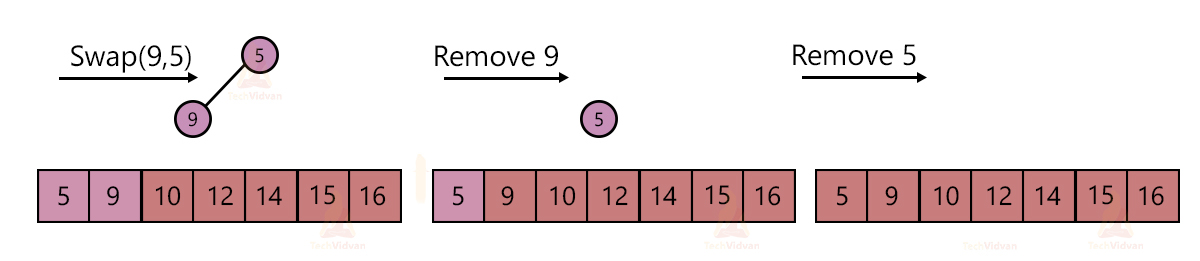
In a max-heap, the root node contains the largest element. In every step, we will pick up the element at the root node, i.e. the largest element and place it at the end of the array.

This mainly involves three steps followed repeatedly to sort the array.

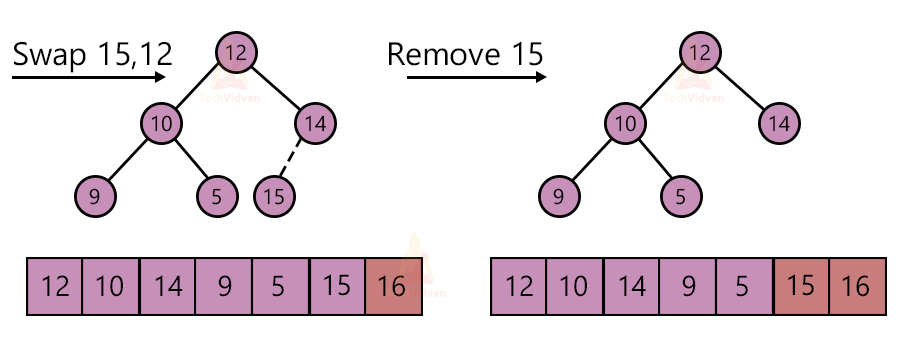
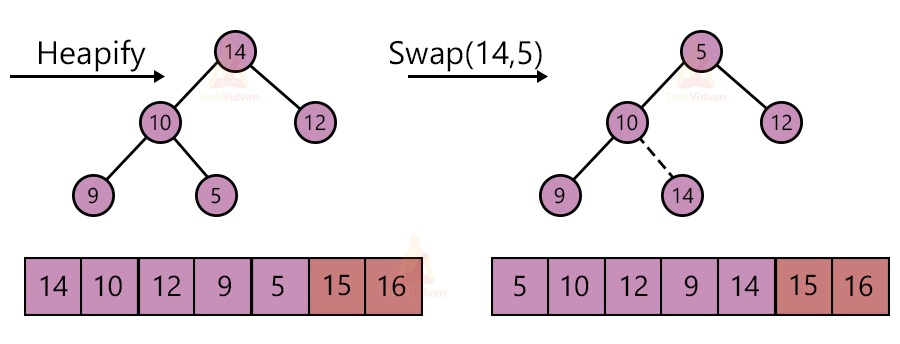
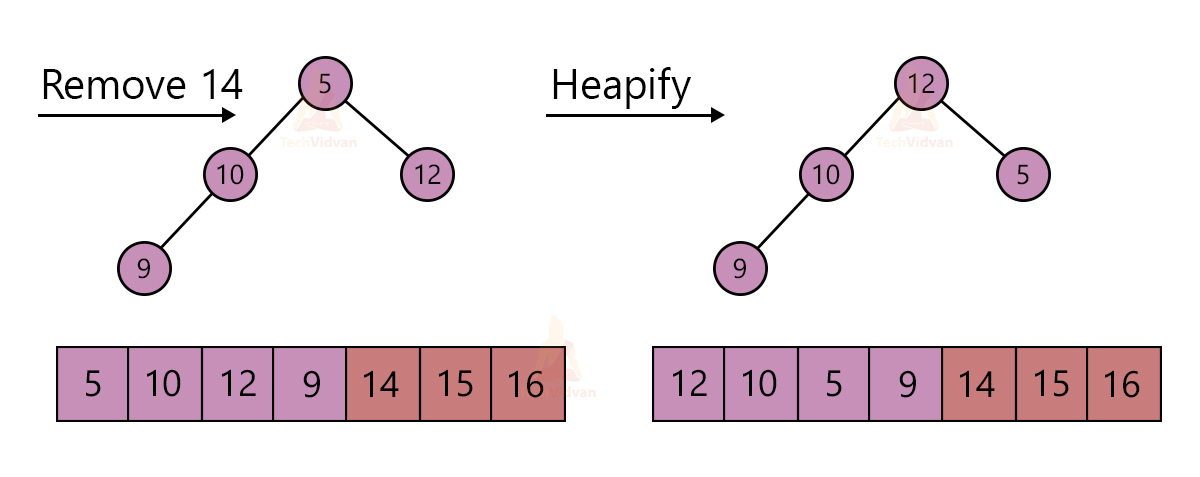
1. Take the root node element and replace it with the last element of the heap.

2. Remove the largest element from the heap. Decrement the size of the heap by one.

3. Apply the heapify algorithm to make it a max-heap again.

Heapify Algorithm

Heapify

Heapify Working

Heapify Algorithm

Heapsort working

Heapsort implementation

Heapify in DS

Heapsort in Data Structure

Heapsort working

Thus, the final sorted array comes out to be:

heapsort output

Heapsort Procedure:

procedure Heap_sort(A, n):
    Build_heap(A, n)
    for (i=n; i>=2; i--):
        swap(A[i], A[1])
        n = n - 1
        Heapify(A, 1, n)
    END for loop
END Heap_sort

Implementation of Heapsort in C:

#include <stdio.h>

void swap(int *num1, int *num2) {
    int temp = *num1;
    *num1 = *num2;
    *num2 = temp;
  }

void Heapify(int array[], int n, int i)
{
  int max = i; 
  int Left = 2 * i + 1;
  int right = 2 * i + 2; 
  if (Left < n && array[Left] > array[max])
    max = Left;
  if (right < n && array[right] > array[max])
    max = right;
  if (max != i)
  {
    swap(&array[i], &array[max]);
    Heapify(array, n, max);
  }
}

void Heap_sort(int Arr[], int n)
{
  for (int i = n / 2 - 1; i >= 0; i--)
    Heapify(Arr, n, i);
  for (int i = n - 1; i > 0; i--)
  {
    swap(&Arr[0], &Arr[i]);
    Heapify(Arr, i, 0);
  }
}

void Dispay_array(int arr[], int n)
{
  for (int i = 0; i < n; ++i)
    printf("%d" , arr[i]);
  printf("\n");
}

int main()
{
  int array[] = {24, 12, 1, 20, 16, 8, 30};
  int n = sizeof(array) / sizeof(array[0]);

  Heap_sort(array, n);

  printf("Sorted array is: \n");
  Dispay_array(array, n);
}

Heap sort Implementation in C++

#include <bits/stdc++.h>
using namespace std;
void swap(int *num1, int *num2) {
    int temp = *num1;
    *num1 = *num2;
    *num2 = temp;
  }

void Heapify(int array[], int n, int i)
{
  int max = i; 
  int Left = 2 * i + 1;
  int Right = 2 * i + 2; 
  if (Left < n && array[Left] > array[max])
    max = Left;
  if (Right < n && array[Right] > array[max])
    max = Right;
  if (max != i)
  {
    swap(array[i], array[max]);
    Heapify(array, n, max);
  }
}

void Heap_sort(int Arr[], int n)
{
  for (int i = n / 2 - 1; i >= 0; i--)
    Heapify(Arr, n, i);
  for (int i = n - 1; i > 0; i--)
  {
    swap(Arr[0], Arr[i]);
    Heapify(Arr, i, 0);
  }
}

void Dispay_array(int arr[], int n)
{
  for (int i = 0; i < n; ++i)
    cout << arr[i] << " ";
  cout << "\n";
}

int main()
{
  int array[] = {24, 12, 1, 20, 16, 8, 30};
  int n = sizeof(array) / sizeof(array[0]);

  Heap_sort(array, n);

  cout << "Sorted array is: \n";
  Dispay_array(array, n);
}

Implementation of Heap Sort in Java:

public class Heap_sorting {
  public void H_sort(int Arr[])
  {
    int n = Arr.length;
    for (int i = n / 2 - 1; i >= 0; i--)
      Heapify(Arr, n, i);

    for (int i = n - 1; i > 0; i--)
    {
      int temp = Arr[0];
      Arr[0] = Arr[i];
      Arr[i] = temp;
      Heapify(Arr, i, 0);
    }
  }
  
  void Heapify(int arr[], int n, int i)
  {
    int max = i; 
    int Left = 2 * i + 1; 
    int Right = 2 * i + 2; 
    if (Left < n && Arr[l] > Arr[max])
      max = l;
    if (Right < n && Arr[Right] > Arr[max])
      max = Right;
    if (max != i) {
      int swap = Arr[i];
      Arr[i] = Arr[max];
      Arr[max] = swap;
      Heapify(Arr, n, max);
    }
  }

  static void Display_array(int arr[])
  {
    int n = arr.length;
    for (int i = 0; i < n; ++i)
      System.out.print(arr[i] + " ");
    System.out.println();
  }

  public static void main(String args[])
  {
    int arr[] = {24, 12, 1, 20, 16, 8, 30};
    int n = arr.length;

    Heap_sorting ob = new Heap_sorting();
    ob.H_sort(arr);
    System.out.println("Sorted array is");
    Display_array(arr);
  }
}

Heapsort Implementation in Python:

def Heapify(Arr, n, i):
  max = i 
  Left = 2 * i + 1	 
    Right = 2 * i + 2	 
  if Left < n and Arr[max] < Arr[l]:
    max = Left
  if Right < n and Arr[max] < Arr[r]:
    max = Right
  if max != i:
    Arr[i], Arr[max] = Arr[max], Arr[i] 
    Heapify(Arr, n, max)

def Heap_sort(Arr):
  n = len(Arr)
  for i in range(n//2 - 1, -1, -1):
    Heapify(Arr, n, i)
  for i in range(n-1, 0, -1):
    Arr[i], Arr[0] = Arr[0], Arr[i] 
    Heapify(Arr, i, 0)

list = [24, 12, 1, 20, 16, 8, 30]
Heap_sort(list)
n = len(list)
print("Sorted array is: ")
for i in range(n):
  print("%d" % list[i])

Complexity of Heapsort:

The heapify process takes log n time and the swapping takes O(n) time. Thus the overall time complexity of heapsort is O(n logn).

Scenario  Time complexity
Worst case O(n logn)
Average case O(n logn)
Worst case O(n logn)

The space complexity of heapsort is of order O(1) but the overhead due to recursion is very large.

Applications of Heapsort:

  • This is used to find the kth largest element or kth smallest element from a given list.
  • It is used to find the k largest elements in a list/array.
  • It is used to find the k smallest elements in an array or a list.
  • Heapsort is used in embedded systems. It is also used in places where security is the main concern.

Conclusion:

This article covers everything that you need to know about the heap sort algorithm. In this article, we have taken a look into the heap data structure, the heapify algorithm and heapsort. We have seen the working and implementation of the heapsort algorithm as well.