Insertion Sort in Data Structure
Insertion sort is a comparison-based sorting algorithm mostly suited for small datasets. Insertion sort has wide practical implementations. For example, sorting of play cards is an implementation of insertion sort. Arranging randomly arranged answer sheets in the ascending order of roll numbers is also an example of insertion sort.
What is Insertion Sort?
In insertion sort, there are two lists in the array at every point: A partially sorted list and an unsorted list. Thus, we virtually split the array into sorted and unsorted parts.
Every time we pick up an element from the unsorted array and place it in the partially sorted array. Thus, we insert the elements from an unsorted array at their correct position in the sorted array. That is why the name Insertion. It is not suitable for very large datasets.
Insertion sort is a stable element. The order of duplicate elements is preserved after the sorting is performed.
Insertion Sort Algorithm
Step 1: For i = 1 to n-1
Step 2: Set temp = array[i]
Step 3: Set j = i-1
Step 4: while temp <= array[j]
Set array[j + 1] = array[j]
Set j = j-1
Step 5: Set array[j + 1] = temp
Step 6: END
Insertion Sort Pseudo-code
Procedure Insertion_sort(int Arr)
int insert_at_position, insert_value;
for int i = 1 to length.Arr :
insert_value = Arr[i]
insert_at_position = i
while insert_at_position > 0 and Arr[insert_at_position-1] > insert_value:
Arr[insert_at_position] = Arr[insert_at_position-1]
insert_at_position = insert_at_position -1
END while
Arr[insert_at_position] = insert_value
END for
END procedure
Working of Insertion Sort
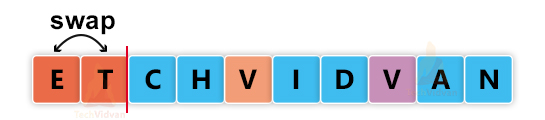
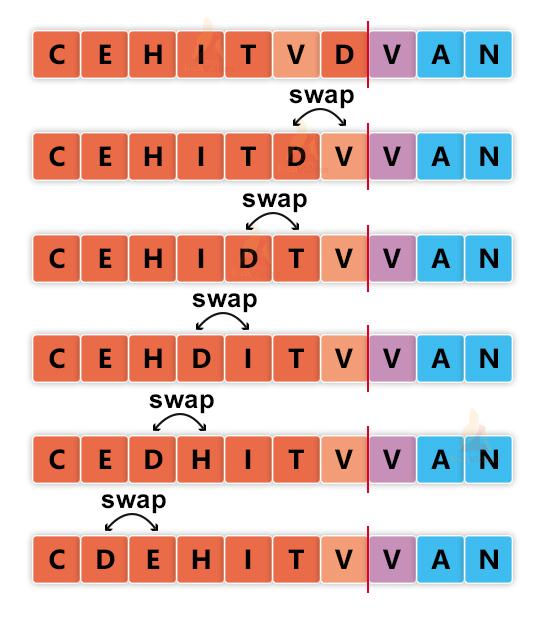
Let us understand the working of insertion sort with the help of an example. Suppose we wish to sort the elements of the word “TECHVIDVAN” in alphabetical order. Then, we will proceed as follows:
In each iteration, we will bring one element from the unsorted list to the sorted list and place it at its correct position.
Iteration 1:
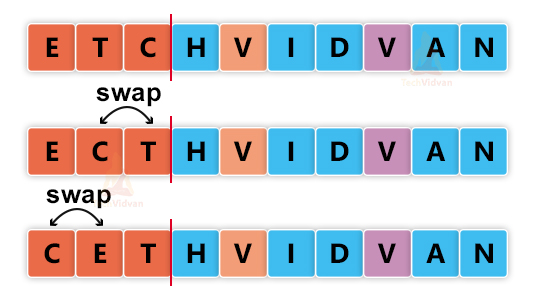
Iteration 2:
Iteration 3:
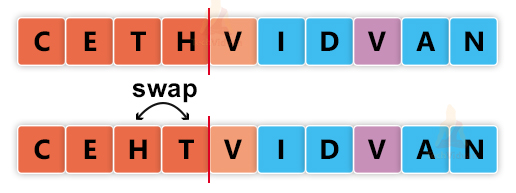
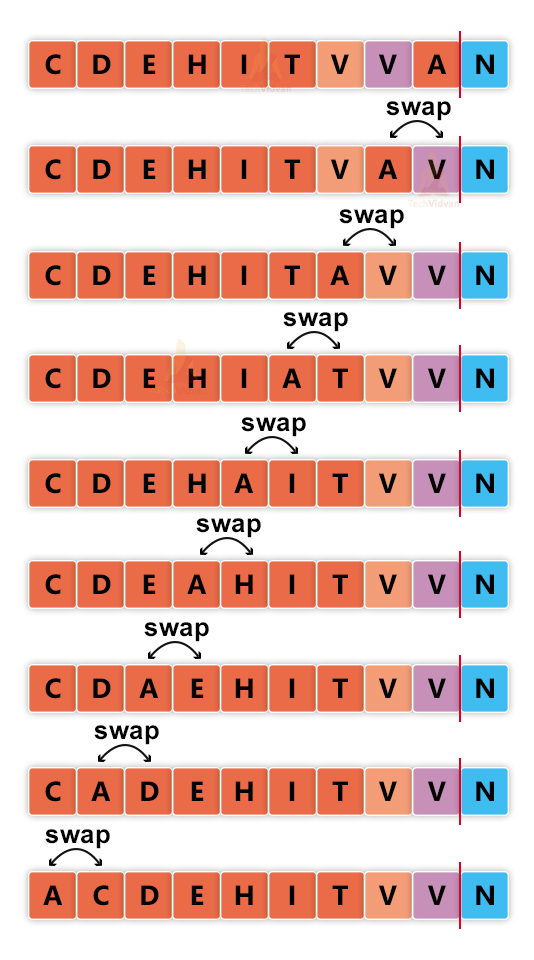
Iteration 5:
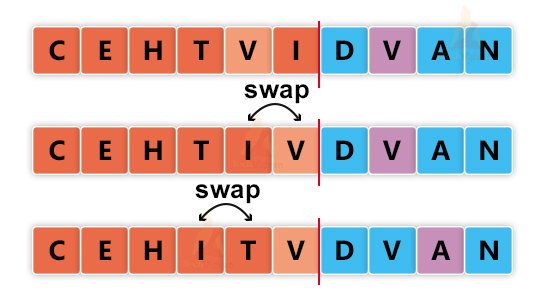
Iteration 6:
Iteration 7:
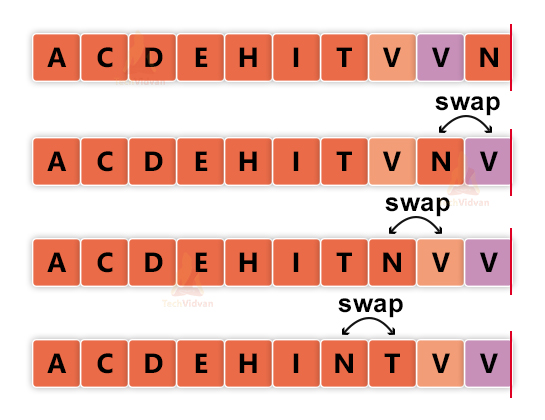
Iteration 9:
Finally, after the 9th iteration, we have got the sorted array.
We need to note here that the insertion sort is a stable sorting algorithm. Thus, the order of duplicates is preserved. Here, we have two duplicate elements- ‘V’. thus, the order of both the ‘V’s will remain the same before and after sorting.
Insertion Sort Implementation in C
#include <stdio.h>
void Insertion_sort(int Arr[], int n)
{
for (int position=1; position<size; position++)
{
int val = Arr[position];
int j = position - 1;
while (val < Arr[j] && j >= 0)
{
Arr[j+1] = Arr[j];
--j;
}
Arr[j + 1] = val;
}
}
int main()
{
int Arr[] = {20, 80, 12, 34, 1, 56, 100, 7, 21, 15};
int len = sizeof(Arr) / sizeof(Arr[0]);
Insertion_sort(Arr, len);
printf("The sorted array is: \n");
for (int index = 0; index < len; index++)
printf("%d ", Arr[i]);
printf("\n");
}
Insertion Sort Implementation in C++
#include <bits/stdc++.h>
using namespace std;
void Insertion_sort(int Arr[], int n)
{
for (int position = 1; position<n; position++)
{
int val = Arr[position];
int j = position - 1;
while (val < Arr[j] && j >= 0)
{
Arr[j+1] = Arr[j];
--j;
}
Arr[j + 1] = val;
}
}
int main()
{
int Arr[] = {20, 80, 12, 34, 1, 56, 100, 7, 21, 15};
int len = sizeof(Arr) / sizeof(Arr[0]);
Insertion_sort(Arr, len);
cout << "Sorted array:\n";
for (int i = 0; i < len; i++)
{
cout << "The sorted arrayis: " << Arr[i];
}
cout << "\n";
return 0;
}
Implementation of Insertion Sort in Java
public class insertionSort
{
void Insertion_sort(int Arr[])
{
int len = Arr.length;
for (int position = 1; position<len; position++)
{
int val = Arr[pos];
int j = position - 1;
while (j >= 0 && val < Arr[j])
{
Arr[j + 1] = Arr[j];
--j;
}
Arr[j + 1] = val;
}
}
public static void main(String args[])
{
int data[] = {20, 80, 12, 34, 1, 56, 100, 7, 21, 15};
insertionSort is = new insertionSort();
is.Insertion_sort(data);
System.out.println("The sorted Array is: ");
for (int i=0;i<data.length; i++)
System.out.print(data[i] + " ");
}
}
Insertion Sort Implementation in Python
def Insertion_sort(Arr):
for position in range(1, len(Arr)):
value = Arr[position]
j = position - 1
while j >= 0 and value < array[j]:
Arr[j + 1] = Arr[j]
j = j - 1
Arr[j + 1] = value
list = [20, 80, 12, 34, 1, 56, 100, 7, 21, 15]
Insertion_sort(list)
print('The sorted Array is:')
print(list)
Complexity Analysis of Insertion Sort
The time complexity of the insertion sort algorithm is mainly dependent on two operations- the number of comparison operations and the number of swaps.
For insertion sort, the time complexities are:
| Scenario | Time complexity |
| Best case | O(1) |
| Average case | O(n2) |
| Worst case | O(n2) |
The space complexity for insertion sort is O(1).
Insertion Sort for Singly Linked List
A singly-linked list is a linear data structure. Hence, just like an array, we can apply insertion sort on the linked list elements as well.
The following steps need to be followed:
1: The first step is to create an empty list, which will always be sorted.
2: Start traversing the list.
3: As we traverse the list, insert the current node each time, in a sorted way into the linked list.
4: Point the head of the given list to that of the sorted linked list.
Insertion Sort Implementation for Linked List using C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node* Next;
Node(int x)
{
key = x;
Next = NULL;
}
};
class LinkedList {
public:
Node* Head;
Node* sorted_list;
void Push(int key)
{
Node* New_node = new Node(key);
New_node->Next = Head;
Head = New_node;
}
void Insertion_sort(Node* Head_ref)
{
sorted_list = NULL;
Node* current = Head_ref;
while (current != NULL) {
Node* Next = current->Next;
Insert_into_sorted(current);
current = Next;
}
Head = sorted_list;
}
void Insert_into_sorted(Node* New_node)
{
if (sorted_list == NULL || sorted_list->key >= New_node->key) {
New_node->Next = sorted_list;
sorted_list = New_node;
}
else {
Node* current = sorted_list;
while (current->Next != NULL && current->Next->key < New_node->key) {
current = current->Next;
}
New_node->Next = current->Next;
current->Next = New_node;
}
}
void Display_list(Node* Head)
{
while (head != NULL) {
cout << Head->key << " ";
Head = Head->Next;
}
}
};
int main()
{
LinkedList list;
list.Head = NULL;
list.push(10);
list.push(40);
list.push(8);
list.push(7);
list.push(52);
cout << "Before sorting, the linked list is: " << endl;
list.Display_list(list.Head);
cout << endl;
list.Insertion_sort(list.Head);
cout << "Linked List After sorting: " << endl;
list.Display_list(list.Head);
}
Implementation of Insertion Sort for Linked List using Java:
public class LinkedList
{
node Head;
node sorted_list;
class node
{
int key;
node Next;
public node(int key)
{
this.key = key;
}
}
void Push(int key)
{
node New_node = new node(key);
New_node.Next = Head;
Head = New_node;
}
void Insertion_sort(node Head_ref)
{
sorted_list = null;
node current = Head_ref;
while (current != null)
{
node Next = current.Next;
Insert_into_sorted(current);
current = Next;
}
Head = sorted_list;
}
void Insert_into_sorted(node New_node)
{
if (sorted_list == null || sorted_list.key >= New_node.key)
{
New_node.Next = sorted_list;
sorted_list = New_node;
}
else
{
node current = sorted_list;
while (current.Next != null && current.Next.key < New_node.key)
{
current = current.Next;
}
New_node.Next = current.Next;
current.Next = New_node;
}
}
void Display_list(node Head)
{
while (Head != null)
{
System.out.print(Head.key + " ");
Head = Head.Next;
}
}
public static void main(String[] args)
{
LinkedList list = new LinkedList();
list.push(10);
list.push(40);
list.push(8);
list.push(7);
list.push(52);
System.out.println("Linked List before Sorting is:");
list.Display_list(list.Head);
list.Insertion_sort(list.Head);
System.out.println("\nLinkedList After sorting is:");
list.Display_list(list.Head);
}
}
Insertion Sort Implementation for Linked List using Python:
class Node:
def __init__(self, key):
self.keya = key
self.Next = None
def Insertion_sort(Head_ref):
sorted_list = None
current = Head_ref
while (current != None):
Next = current.Next
sorted_list = Insert_into_sorted(sorted_list, current)
current = Next
Head_ref = sorted_list
return Head_ref
def Insert_into_sorted(Head_ref, New_node):
current = None
if (Head_ref == None or (Head_ref).key >= New_node.key):
New_node.Next = Head_ref
Head_ref = New_node
else:
while (current.Next != None and current.Next.key < New_node.key):
current = current.Next
New_node.Next = current.Next
current.Next = New_node
return Head_ref
def Display_list(Head):
temp = Head
while(temp != None):
print( temp.key, end = " ")
temp = temp.Next
def push( head_ref, new_data):
New_node = Node(0)
New_node.key = New_key
New_node.Next = (Head_ref)
(Head_ref) = New_node
return Head_ref
a = None
a = push(a, 10)
a = push(a, 40)
a = push(a, 8)
a = push(a, 7)
a = push(a, 52)
print("Linked List before sorting is: ")
Display_list(a)
a = Insertion_sort(a)
print("\nLinked List after sorting is: ")
Display_list(a)
Applications of Insertion Sort
- Insertion sort is the best algorithm when the number of elements is small i.e. for a small input size.
- Insertion sort is also the best when the data is already sorted. This is because insertion sort takes the least execution time in such a case as compared to other sorting techniques.
- When we don’t have access to all the data initially, we use insertion sort. This is because insertion sort never requires all the elements at a time for sorting. Thus, it is best suitable when the data is arriving one by one.
Conclusion
Insertion sort in another sorting algorithm useful for small input size. It is best suited when we have online data i.e. the data arriving one by one. It is a stable sorting algorithm with a time complexity of O(n2).
In this article, we have learned the basic idea behind insertion sort. We have also seen the working and the implementation of insertion sort in various programming languages.