Linear Search in Data Structure

Searching is a technique used to find out a particular element from a given list of elements. We can perform searching on any data structure such as arrays, linked lists, trees, graphs, etc.

If the element we are searching for is present in the list/data structure, the searching technique returns success. Otherwise, the search is considered unsuccessful.

There are three popular search methods:
1. Linear search
2. Binary search
3. Interpolation search

Out of these searching techniques, the first two are more popular and widely used. Let us discuss one of them in this article.

Linear Search

It is also known as sequential search. As the name suggests, in linear search, we sequentially traverse all the elements.

If we can find the element we were searching for, the linear search algorithm returns the address/location of that element in the list. Otherwise, the algorithm returns NULL. We mostly used linear search whenever the list is unsorted.

How Linear Search Works?

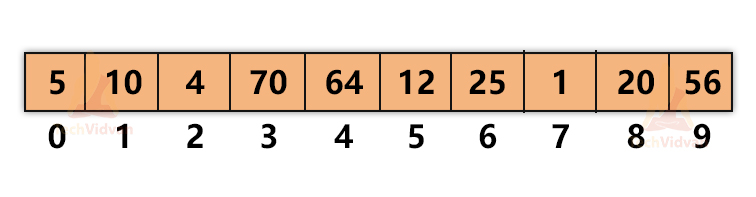
Consider an array containing 10 elements as shown:

Suppose that the element we wish to search is ‘x’. There will be two possible cases: we will either find ‘x’ in the list or not find ‘x’ in the list. If x is present in the list, the algorithm will return the index of that location, otherwise, it will return some invalid address.

Let us see both of these cases:

1. In case of success:

Suppose the value of ‘x’ is 12. We know that 12 is present in the array. The algorithm will start searching for 12 linearly starting from the beginning. It will first check the 0th index, compare the element at the 0th index with 12, if 12 is present there, it will return 0, else move to the next location.

Here, 12 is not present at the 0th index. Therefore, the algorithm moves to the 1st index, following the same procedure. Then it moves to the next position. This traversal will continue in the same manner until we reach the 5th index and finally, the algorithm will return 5.

2. In case of failure:

Suppose that the value of ‘x’ is 50. 50 is not present anywhere in the list. In this case, the algorithm will linearly traverse the whole array and in the end, it will return NULL.

Example:
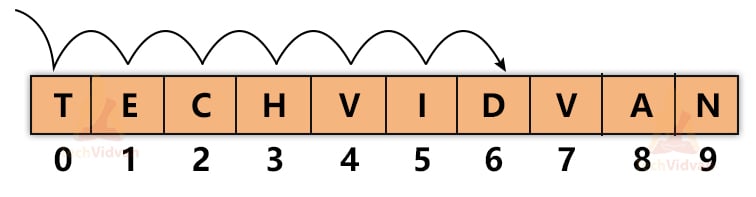
Let the input array be: {‘T’, ‘E’, ‘C’, ‘H’, ‘V’, ‘I’, ‘D’, ‘V’, ‘A’, ‘N’}. Suppose we wish to search ‘D’ from the array. We will start traversing from the beginning as shown:

Output: 6 (the index of the element).

Algorithm for Linear Search

Step1: Initialize i := 1;
Step2: if (i>n) exit;
Step3: Repeat step4 to step5 while i<=n;
Step4: If A[i] == x, print i;
Step5: Set i := i+1;
Step6: Else print element not found;
Step7: Exit;

Pseudo-code of Linear Search

int Linear_Search(list, key)
{
    for(i=0; i<n; i++)
    {
        if(A[i] == key)
            return i;
    }
}

Complexity of Linear Search

The space complexity for the linear search algorithm in every case is O(1). Time complexity is different in different cases and varies according to the input.

The following table gives the time complexity of the linear search algorithm:

Case	Time complexity
Best case	O(1)
Average case	O(n)
Worst case	O(n)

Linear search implementation in C:

int Linear_search(int arr[], int n, int key)
{
    int i;
    for (i = 0; i<n; i++)
        if (arr[i] == key)  //key is the lement to be searched
            return i;
    return -1;  //when the element is not present inside the array
}
 
 
int main(void)
{
    int arr[] = { 5, 3, 6, 2, 20, 7};
    int key = 20;
    int n = sizeof(arr) / sizeof(arr[0]);
   
    
    int result = Linear_search(arr, n, key);
    if(result == -1)
        printf("Element is not present in array")
    Else
        printf("Element is present at index %d", result);
    return 0;
}

Implementation of Linear Search In C++

#include <iostream>
using namespace std;
 
int Linear_search(int arr[], int n, int key)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
    return -1;
}
 
int main(void)
{
    int arr[] = {10, 15, 2, 43, 21, 15};
    int key = 10;
    int n = sizeof(arr) / sizeof(arr[0]);
   
    int  result = Linear_search(arr, n, key);
    if (result == -1)
        cout << "Element is not present in array"
    else
        cout << "Element found at location " << result+1;
    return 0;
}

Linear Search Implementation in Java

class TechVidvan
{
    public static int Linear_search(int arr[], int key)
    {
        int n = arr.length;
        for (int i = 0; i < n; i++)
        {
            if (arr[i] == key)
                return i;
        }
        return -1;
    }
 
   
public static void main(String args[])
    {
        int arr[] = { 12, 15, 20, 3, 5};
        int key = 10;
 
        
        int result = Linear_search(arr, key);
        if (result == -1)
            System.out.print(
                "Element is not present in array");
        else
            System.out.print("Element is present at index "
                             + result);
    }

Implementation of Linear Search in Python:

def Linear_search(arr, n, key):
 
    for i in range(0, n):
        if (arr[i] == key):
            return i
    return -1
 
arr = [12, 3, 24, 10, 4]
key = 10
n = len(arr)
 
result = Linear_search(arr, n, key)
if(result == -1):
    print("Element is not present in array")
else:
    print("Element is present at index", result)

Conclusion

Whenever we have lots of data in a list and we need to search for one particular item, we need a searching method. Linear search is used whenever the list is unsorted.

This article studied the linear search algorithm and how it is implemented to search for items in a given list.