Queue in Data Structure
The queue data structure is linear. It follows the FIFO approach i.e. First In First Out or Last In Last Out.
In the queue, the order of insertion is the same as the order of deletion of elements because of the FIFO approach.
Queues are mostly used whenever there is a single resource and multiple users want to use that resource. For example, in threads and CPU scheduling algorithms.
A data structure queue is analogous to a queue in real life. For example, people waiting in a queue to buy movie tickets.
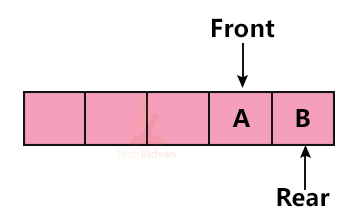
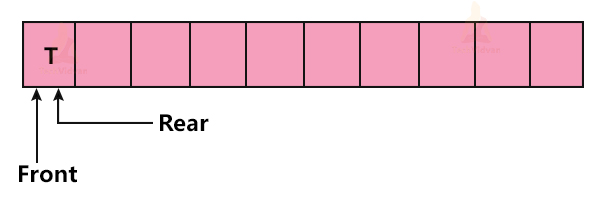
Representation of a Queue
Just like a stack, the queue is also an abstract data type but it follows the FIFO approach. In the queue, we always remove the least recently added element.
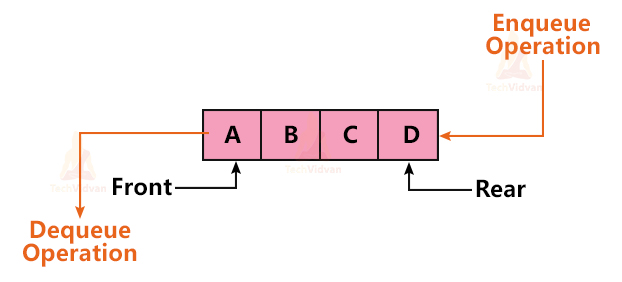
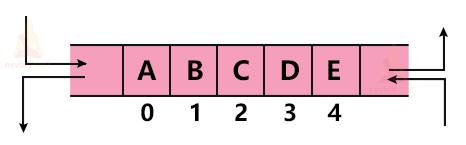
A queue is open at both ends, unlike a stack. Thus we perform deletion and insertion operations at two different ends in a queue.The two ends of the queue are the Front and Rear respectively.
Front points to the index of the queue from where we can delete an element. Rear points to that index of the queue from where we insert elements.
We can represent the queue as follows:
Types of Queue
There are various types of queue data structures such as:
1. Linear queue
2. Circular queue
3. Deque
4. Priority queue
Let us see each of them in detail now:
1. Linear queue
A linear queue is a simple queue in which insertion occurs at one end and deletion occurs at the other end.
In a linear queue, we are sometimes not able to utilize memory effectively. This is because insertion can be performed only at the rear end.
Basic operations on Linear Queue:
The basic operations that we can perform on a queue are:
a. enqueue(): To insert an element into the queue.
b. dequeue(): To delete an element from a queue.
c. peek(): To print/display the element at the front without deleting it.
d. isfull(): To check if the queue is full or not.
e. isempty(): To check if the queue is empty or not.
Out of the given operations, the first two operations are the most important. The rest three are used to improve the efficiency of the first two operations while implementation.
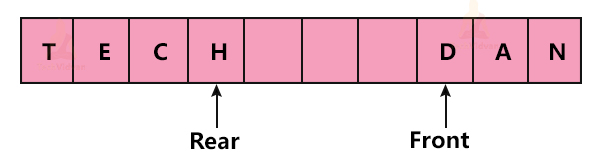
a. enqueue() Operation in Queue
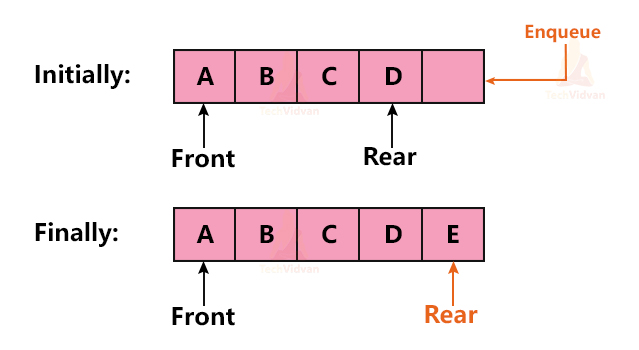
The queue has two ends pointed by Front and Rear. The enqueue() operation is always performed at the Rear end.
While performing enqueue() operation, we always check whether the queue is full or not. In case the queue is full, we return an overflow error. Otherwise, we insert the element at the rear end and make the Rear point to the next position in the queue.
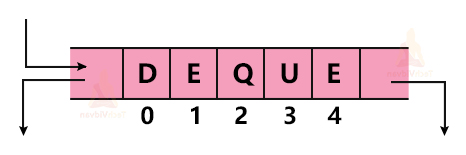
For example, suppose we have a queue with elements A, B, C, D and we wish to insert E into the queue. We can insert this new element into the queue as follows:
The pseudo-code for the enqueue() operation is shown below:
void enQueue(int key) //key is the element to be inserted
{
if(Rear == SIZE-1){ //SIZE denotes the maximum size of the queue
print("Overflow"); //Prints overflow if the queue is already full.
return;
}
if(Front == -1){ //If the queue is empty
Front = 0; //whenever the queue is empty, front always point to -1 initially
Rear = 0; //'Queue being empty' is a rare case when both front and rear point to the same index
Queue[Rear] = key;
}
else{
Rear = Rear + 1; //Making rear point to the next index of the queue
Queue[Rear] = key;
}
}
The time complexity of enqueue() operation is of the order O(1).
Thus, in enqueue operation, we need to remember the following key points:
While performing enqueue() operation algorithmically, we check three different cases. These cases are:
- When the queue is empty
- When the queue is full
- Otherwise
When the queue is full, the rear will point to the last index i.e. Size of queue – 1 position. In that case, we will return an overflow error and exit the program.
When the queue is empty, initially both the front and rear will point to an invalid index say -1. In this case, when we insert an element, both will start pointing to index 0.
Since the queue has only one element, in this case, both the front and rear for a queue will be the same.
If the queue is neither empty nor full, we just increase the value of the rear pointer by one and insert the new element.
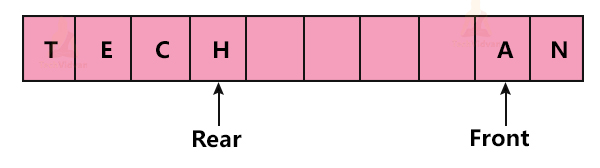
b. dequeue() Operation
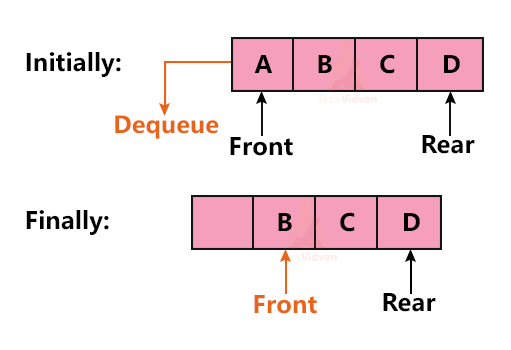
This operation is used to delete an element from the queue. dequeue() operation is always performed at the ‘Front’ of the queue.
While performing dequeue() operation, we always make sure that the queue is not already empty. If the queue is already empty, there is nothing to delete. In that case, we return an underflow error. If the queue is not empty, we delete the front node and move the front pointer to the next node.
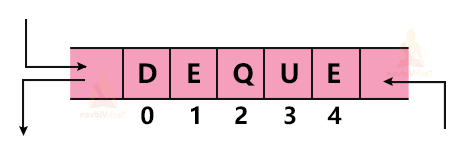
The following diagram depicts the deletion operation:
The pseudo-code for dequeue() operation is:
int deQueue()
{
int temp; //We declare 'temp' variable to store the value of element to be deleted
if(Front == -1) //If the queue is empty
{
printf("Underflow");
break;
}
if(Front == Rear) //If the queue has only one element
{
temp = Queue[Front];
Front = -1;
Rear = -1;
return temp;
}
else
{
temp = Queue[Front];
Front = Front + 1;
return temp;
}
}
The time complexity of the dequeue() operation is O(1) when we implement the queue using arrays.
In case of dequeue() operation:
- If the queue is empty, the Front will be pointing to an invalid index. In this case, we will return the underflow error and exit the program.
- If the queue contains only one element, both the Front and Rear will point to the same index. In this case, we will delete the element and make the front and rear point to any invalid index.
c. isfull() Operation in Queue
Whenever the rear points to the SIZE (i.e. the maximum size of the queue), the isfull() operation returns true.
isfull() operation is a boolean operation i.e. it either returns true or false.
The code for the isfull() operation is as shown below:
bool isfull() {
if(Rear == SIZE-1)
return true;
else
return false;
}
d. isEmpty() Operation
It will return true only if the queue is empty. Just like isfull() operation, it is a boolean operation and so it returns either true or false.
If the value of the Front is MIN or pointing to an invalid index, then the queue is empty. Thus, this operation will return true.
The code for isEmpty() operation is:
bool isEmpty() {
if(000Front < 0 || Front > Rear)
return true;
else
return false;
}
e. peek() Operation in queue
This operation returns the value of the data element at the front of the queue without deleting it. Its code will be:
int peek() {
return Queue[Front];
}
Applications of Linear Queue
Queues are mainly used for ordering items into a particular order of performance or when there are multiple users for a single resource.
The major applications of the queue data structure are:
1. Asynchronous data transfer
We can make use of queues to transfer data asynchronously. Asynchronous transfer means when the rate of transmission of data is not the same between two processes. For example, queues are used in pipes, file input/output, sockets for asynchronous data transfer.
2. Multiple users for a single resource
Whenever we need to make the process wait for a single shared resource, we maintain them inside a queue. For example, printer, CPU, etc are the shared resources.
3. Used as buffers
Queues are useful as a buffer to store the data primarily whenever required. For example, the queue is used as a buffer in the case of MP3 players. CD players, etc.
4. Interrupt handling
Whenever a process gets interrupted, it is sent back and made to wait in the queue. Thus, queue helps in interrupt handling.
5. Maintain playlists
Queues help maintain any kinds of lists. We can maintain a playlist of songs or other media with the help of queues.
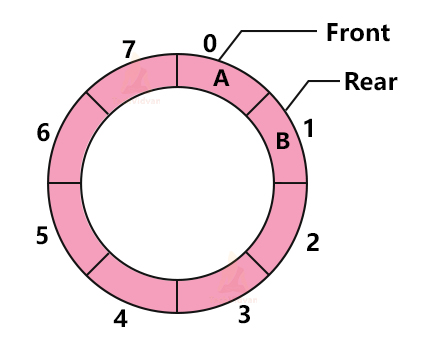
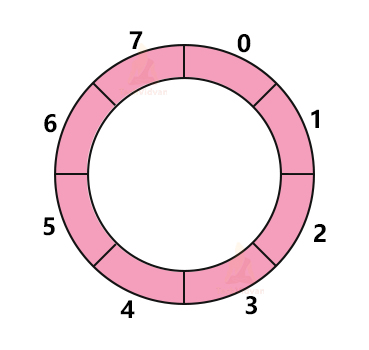
Circular Queue
A circular queue overcomes the drawback of a linear queue. In the circular queue, all the nodes are in a circle interconnected to each other. The last element of the queue is connected to the first element. It also follows the FIFO approach. It is also known as the Ring buffer.
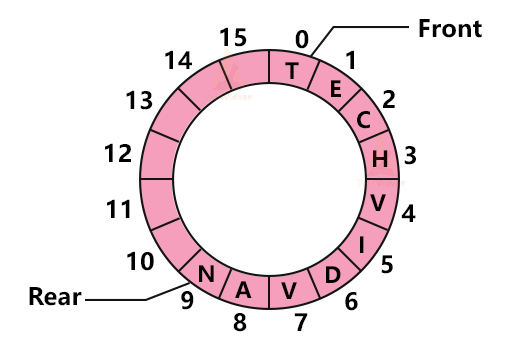
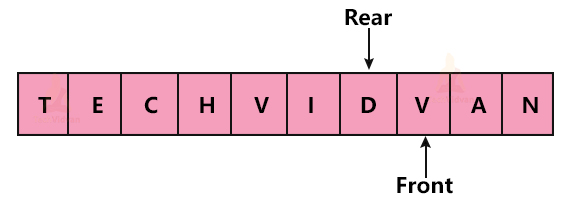
Representation of Circular queue:
Suppose we have the letters of the word “TECHVIDVAN”. It will be represented in the circular queue as follows:
Operations on Circular queue:
Following are the operations that we can perform on circular queues:
1. Front( ): It returns the element at which the front pointer is pointing.
2. Rear( ): It returns the last element of the circular queue.
3. Enqueue( ): It helps to insert a new element at the rear end of the queue.
4. Dequeue( ): It deletes the last element of the circular list from the front end.
Array implementation of Circular queue:
1. Enqueue( ):
If the queue is full, return overflow. If the queue is empty, the rear and front both will point to -1 initially. Insert the new element at 0, and point both front and rear to the 0th index.
Otherwise, insert the lament and increment rear by one.
The pseudo-code will be as follows:
Enqueue_operationint key(){
if (rear+1)%max = front
{
print("overflow");
break;
}
if (front == -1 && rear == -1)
{
front = rear = 0;
CircularQueue[Rear] = key;
}
else
{
Rear = Rear+1;
set CircularQueue[Rear] = key;
}
}
Implementation of Enqueue in C:
void Enqueue(int key)
{
if(Front==-1 && Rear==-1)
{
Front = Rear = 0;
Counter = 1;
CircularQueue[Rear] = key;
}
else if((rear+1) % max == Front)
{
printf("OverFlow");
break;
}
else
{
Rear = (Rear+1) % max;
CircularQueue[Rear] = key;
Counter++;
}
}
2. Dequeue( ):
It helps to delete elements from the rear end.
If the queue is already empty, return underflow. Otherwise, delete the element and decrement the value of the rear by one.
While removing the last element, set both front and rear =-1.
The pseudo-code of the dequeue function is:
Dequeue_operation{
if (Front == -1)
{
display("underflow");
break;
}
if (Front == Rear)
{
Front = Rear = -1;
}
else{
if(Front = SIZE-1)
Front = 0
else
Front = Front + 1
}
}
C implementation of dequeue operation:
int dequeue()
{
int Counter=0;
if(Front == -1 && Rear== -1)
printf("Underflow");
else if(Front == Rear)
{
front=-1;
rear=-1;
Counter=0;
}
else
front=(front+1)%max;
return queue[front];
Counter--;
}
3. size( ):
This operation returns the size of the circular queue. Its implementation in C is shown below:
int size(int Count)
return Count;
Linked List implementation of Circular queue:
We can make use of both arrays as well as linked lists to implement a circular queue. But, the linked list implementation is more efficient. The worst-case time complexity of linked list implementation is O(n).
1. Enqueue( ):
void Enqueue(struct Node* NewNode , int key)
{
NewNode->data = key;
Newnode->Next = 0;
if(Rear==-1)
{
Front = Rear = NewNode;
Rear->Next = Front;
}
else
{
Rear->Next = NewNode;
Rear = NewNode;
Rear->Next = Front;
}
}
2. Dequeue( ):
void Dequeue()
{
if(Front==-1 && Rear == -1)
{
printf("Underflow");
break;
}
else if(Front == Rear)
Front = Rear = -1;
else
{
Front = Front->Next;
Rear->Next = Front;
}
}
3. peek( ):
It returns the value of the element at the front without deleting it.
int peek()
{
if(Front==-1 && Rear==-1)
printf("Underflow- EMpty queue");
else
return Front->data;
}
Applications of Circular queue:
Circular queue comes into use in the following cases:
1. Memory management
Circular queues help in better memory management in comparison to linear queues. A circular queue utilizes unused memory very well. This can be shown as follows:
In this case, even though we have space for 3 elements in the queue, but it will not be able to add the elements. This is because the rear is pointing at the end.
We can overcome this problem using a circular queue as shown:
Since it is circular, we can add elements up to the full capacity of the queue.
2. CPU scheduling
All the processes waiting for their turn can be placed in a circular queue.
3. Traffic system
In computerized traffic systems, circular queues help to switch between the different traffic lights circularly.
Priority queue:
In a priority queue, each element has some priority attached to it. This priority decides the order of execution of nodes inside the queue.
A priority queue is designed in such a way that insertion occurs according to the arrival of elements. The deletion occurs on the basis of the priority of execution.
Types of Priority Queue:
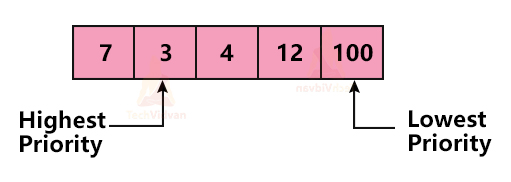
1. Ascending order priority queue: In ascending priority queue, we give higher priority to a smaller number as shown:
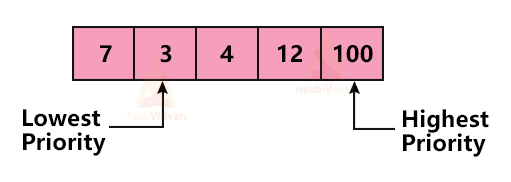
2. Descending order priority queue: It gives high priority to a higher value number.
Implementation of Priority Queue:
We can implement a priority queue using four different data structures:
1. Array
2. Linked list
3. Binary search tree
4. Heap data structure
Heap data structure:
The heap data structure is based on a complete binary tree. It satisfies heap properties. There are two types of heap data structure:
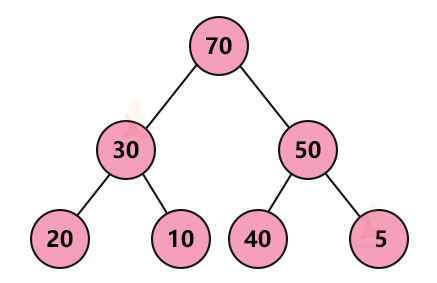
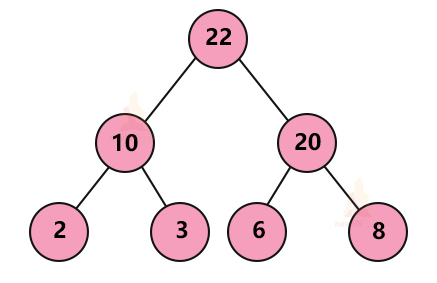
1. Max heap: In a max-heap, for every node, the value of the parent node is greater than both of its child nodes as shown:
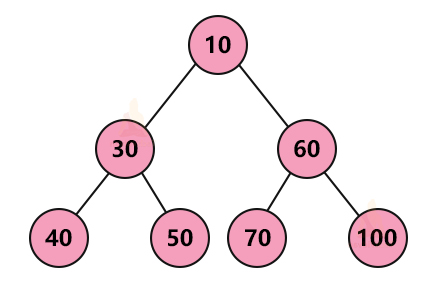
2. Min heap: In a min-heap, the value of every parent node is less than the value of both of its children.
Operations on Priority Queue:
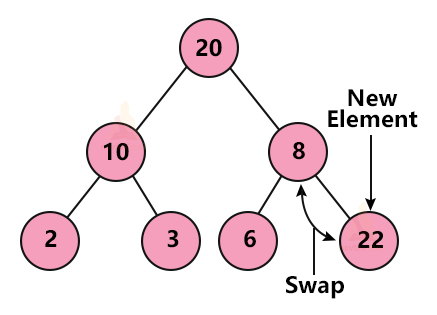
a. Enqueue operation using Max-heap:
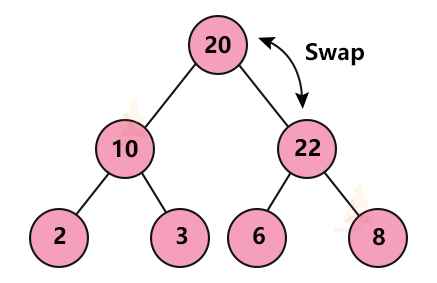
We first insert the element in the available memory slot such that it does not violate the properties of a complete binary tree. If the element is not at the right place i.e. it violates the max-heap property, we compare it to its parent node.
If the value of the parent node is less than the child node, we swap them. These comparisons and swaps continue until all the nodes are in their right place.
Time complexity analysis:
Different data structures generate different time complexities for performing operations on the priority queue.
| Implementation | Insert | Delete | peek |
| Linked list | O(1) | O(n) | O(n) |
| Binary heap | O(log n) | O(log n) | O(1) |
| Binary search tree | O(log n) | O(log n) | O(1) |
Applications of Priority Queue:
A priority queue is useful in the following cases:
1. It helps in the implementation of heapsort.
2. It helps in the implementation of the Huffman code.
3. It is used for finding the shortest path in Dijkstra’s algorithm.
4. It is used in Prim’s algorithm.
5. It helps in the implementation of priority scheduling algorithms in the operating system.
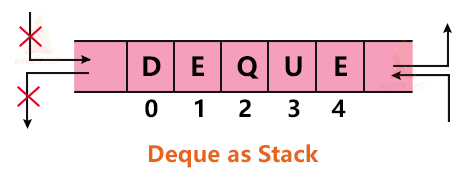
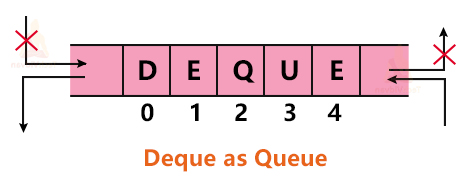
Deque
Deque stands for Double Ended Queue. In deque, we can perform deletion and insertion operations from both ends.
The following diagram represents a deque:
There are two types of deques based on the restrictions imposed:
1. Input-restricted queue: In this type of queue, some restriction is there on the input. We can perform insertion at only one end in an input-restricted queue, but deletion from both ends.
2. Output-restricted queue: In this type of queue, we can perform insertion operation at both ends but deletion at only one end. Thus, it has restrictions on deletion operation.
3. Behaviour as a stack: deque acts as a stack when both insertion and deletion are restricted from the same end.
4. Behaviour as a queue: Deque acts as a queue when we restrict insertion from one end and deletion from the other end.
Operations on Deque:
The basic operations are:
1. Insertion at front
2. Deletion from end
3. Insertion at rear
4. Deletion from rear
5. isFull( )
6. isEmpty( )
We can implement a deque using two data structures:
- Linked lists
- Circular array
A circular array is an array in which the first and the last element are connected to each other as shown:
Array implementation of Deque:
a. Enqueue( ):
If the array is already full, return an overflow error. If the array is empty, set Rear = Front = -1 i.e. make them point to an invalid address.
As we perform the enqueue operation i.e. insert a new element, we increase the value of the rear by 1. If we wish to insert the value at the front, we can apply enqueue operation and decrease the value of the front by 1.
b. Dequeue( ):
If the array is already empty, return an underflow error.
To perform the dequeue operation, we delete the element from the front and decrease the value of the front by 1. If we wish to delete the element from the rear end, we apply a dequeue operation and decrease the value of the rear by 1.
If the rear points to the 0th index while deletion operation, delete the lament and make the rear point to the last element of the circular array.
Working of Deque:
Let us understand the working of a deque with the help of an example.
Consider an array having a maximum size of 10 and we need to insert the word ‘TECHVIDVAN’ in it.
1. When the deque is empty, the front and rear will point to -1.
2. On inserting ‘T’ at the rear, we will have both front and rear pointing to 0.
3. Insert ‘E’, ‘C’ and ‘H’ at the rear and N at the front as shown:
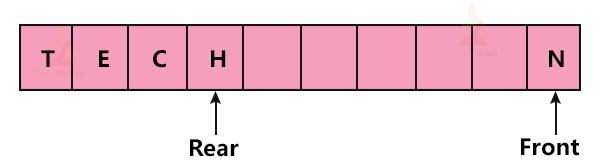4. Insert ‘D’ and ‘A’ at the front.
5. Perform dequeue( ) operation at both front and rear.
6. Insert ‘V’ at the front. Insert ‘H’, ‘V’, ‘I’ and ‘D’ at the rear.
Insertion at the front in Deque:
void Enqueue_at_Front(int key)
{
if(Front==-1 && Rear==-1)
{
Front = Rear = 0;
deque[Front] = key;
}
else if(Front == 0)
{
Front = SIZE-1;
deque[Front] = key;
}
else
{
Front = Front-1;
deque[Front]= key;
}
}
Insertion at the rear in Deque:
void Enqueue_at_Rear(int key)
{
if(Front==-1 && rear==-1)
{
Rear=0;
deque[Rear] = key;
}
else if(Rear == SIZE-1)
{
Rear = 0;
deque[Rear] = key;
}
else
{
Rear++;
deque[Rear] = key;
}
}
Dequeue( ) at the front:
void Dequeue_at_Front()
{
if(Front==-1 && Rear==-1)
{
printf("Underflow");
break;
}
else if(Front == Rear)
{
printf( deque[Front]);
Front=-1;
Rear=-1;
}
else ifFront == SIZE-1)
{
printf(deque[Front]);
Front = 0;
}
else
{
printf(deque[Front]);
Front = Front+1;
}
}
Dequeue( ) at the end:
void Dequeue_at_Rear()
{
if(Front==-1 && Rear==-1)
{
printf("Underflow");
break;
}
else if(Front == Rear)
{
printf(deque[Rear]);
Front = -1;
Rear = -1;
}
else if(Rear == 0)
{
printf(deque[Rear]);
Rear = SIZE-1;
}
else
{
printf(deque[Rear]);
Rear = Rear-1;
}
}
Get front:
int GetFront()
{
if(Front==-1 && rear==-1)
{
printf("Underflow");
return -1;
}
else
return deque[Front];
}
Get rear:
int GetRear()
{
if(Front==-1 && Rear == -1)
{
printf("Underflow");
return -1;
}
else
return deque[Rear];
}
Applications of Deque:
1. It can be useful as both stack and queue.
2. It helps to check whether a string is a palindrome or not.
3. It helps in multiprocessor scheduling. It makes use of the A-steal algorithm for this.
Linear Queue Implementation in C:
Using arrays:
#include <stdio.h>
#define MAXSIZE 5
void Enqueue(int);
void Dequeue();
void Display();
int items[MAXSIZE], Front=-1, Rear=-1;
int main() {
Enqueue(10);
Enqueue(20);
Enqueue(30);
Enqueue(40);
Enqueue(50);
Enqueue(60);
Display();
Dequeue();
Display();
return 0;
}
void Enqueue(int val) {
if (Rear == MAXSIZE-1)
printf("Overflow");
else
{
if(Front == -1)
front = 0;
Rear++;
items[Rear] = val;
printf("\nInserted Value -> %d", val);
}
}
void Dequeue() {
if (Front == -1)
printf("Underflow");
else {
printf("\nDeleted Value : %d", items[Front]);
Front++;
if (Front > Rear)
Front = Rear = -1;
}
}
void Display() {
if (Rear == -1)
printf("Underflow");
else {
printf("\nCurrent elements in Queue :\n");
for (int i = Front; i <= Rear; i++)
printf("%d ", items[i]);
}
printf("\n");
}
Using Linked list:
#include <stdio.h>
#include <stdlib.h>
struct QNode {
int key;
struct QNode* Next;
};
struct Queue {
struct QNode *Front, *Rear;
};
struct QNode* NewNode(int x)
{
struct QNode* temp = (struct QNode*)malloc(sizeof(struct QNode));
temp->key = x;
temp->Next = NULL;
return temp;
}
struct Queue* CreateQueue()
{
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
queue->Front = queue->Rear = NULL;
return queue;
}
void enQueue(struct Queue* queue, int x)
{
struct QNode* temp = NewNode(k);
if (queue->Rear == NULL) {
queue->Front = queue->Rear = temp;
return;
}
queue->Rear->Next = temp;
queue->Rear = temp;
}
void deQueue(struct Queue* queue)
{
if (queue->Front == NULL) // If queue is empty, return NULL.
return;
struct QNode* temp = queue->Front;
queue->Front = queue->Front->Next;
if (queue->Front == NULL)
queue->Rear = NULL;
free(temp);
}
int main()
{
struct Queue* queue = CreateQueue();
enQueue(queue, 10);
enQueue(queue, 20);
deQueue(queue);
enQueue(queue, 25);
enQueue(queue, 63);
deQueue(queue);
enQueue(queue, 120);
deQueue(queue);
printf("Queue Front : %d \n", queue->Front->key);
printf("Queue Rear : %d", queue->Rear->key);
return 0;
}
Conclusion
In this article, we read about the queue data structure, the basic operations performed on the queue, and their implementations. We also read about the use cases and the applications of the queue data structure.