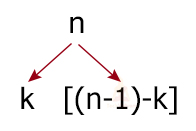Quick Sort in Data Structure

Just like bubble sort and merge sort, quick sort is also a divide and conquer strategy. It is a comparison-based sorting algorithm but not a stable technique. It is an inplace sorting technique. It is also known as a partition-sort exchange algorithm.

What is Quick Sort?

Quicksort is based on a divide and conquer strategy. It works in the following steps:

1. It selects an element from within the array known as the pivot element.
2. Then it makes use of the partition algorithm to divide the array into two sub-arrays. One sub-array has all the values less than the pivot element. The other sub-array has all the values higher than the pivot element.
3. In the next step, the quicksort algorithm calls itself recursively to sort these two sub-arrays.
4. Once the sorting is done, we can combine both the sub-arrays into a single sorted array.

The most important part of quicksort is the partition algorithm. The partition algorithm puts the element into either of the two subarrays depending on the pivot point. We can choose pivot point in many ways:

• Take the first element as the pivot point
• Take the last element of the array as the pivot point
• Take the middle element of the array as the pivot element.
• Take random element as the pivot element in every recursive call

Partition Process in Quick Sort

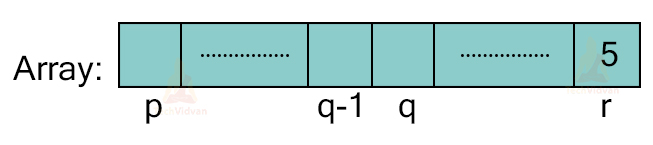
It picks up an element called the pivot element and places that element at its correct position. Let us take the last element of the array to be the pivot element. Then,

Let Pivot = Array[r] and let the correct position of the pivot element 5 be Array[q]. Then, all the elements from Array[p] to Array[q-1] will be less than 5 and all elements from Array[q+1] to Array[r] will be greater than 5.

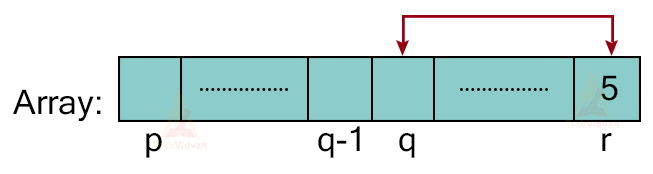
Thus, we will move 5 from Array[r] to Array[q] as shown:

And this process will recursively repeat for all the elements until the array is completely sorted.

Working of Quicksort

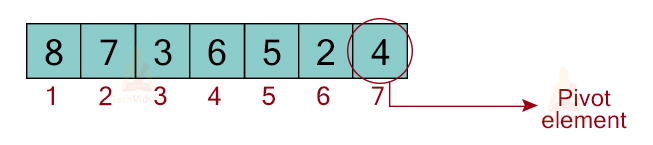
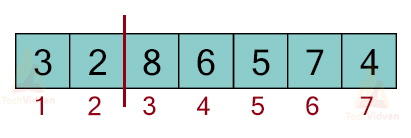
Consider an array having the following elements: 8, 7, 3, 5, 2, 4. Let us choose the last element i.e. 4 as the pivot element.

At position 1, we have 8 and 8>4, therefore, nothing will happen.
At position 2, there is 7 and 7>4, so do nothing.
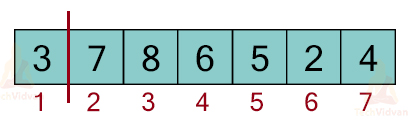
At position 3, the element present is 3 and 3<4. So, we will move 3 to position 1 as shown:

At position 4, we have 6 and 6>4. So, no swapping.
At position 5, 5>4. Again, no swapping.
At position 6, we have 2 and 2<4. So place 2 at position 2 as shown:

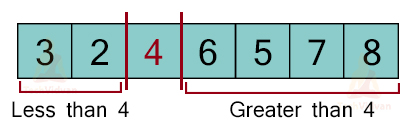
After traversing the whole array and comparing the pivot point with every element, we have found the right position for 4 which is at position 3.

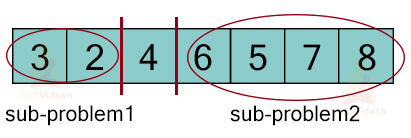
With this step, we have divided the problem into two sub-problems which will again follow the same procedure to sort the elements recursively.

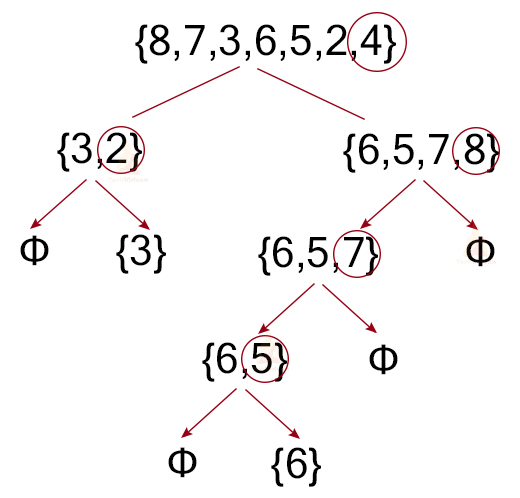
The following recursive tree shows how quicksort will work on all the elements.

Once we have applied the partition procedure on all the elements, the final sorted array will be:

Partition Algorithm

Step 1: Choose the highest index value i.e. the last element of the array as a pivot point
Step 2: Point to the 1st and last index of the array using two variables.
Step 3: Left points to the low index and Right points to the high
Step 4: while Array[Left] < pivot
Move Right
Step 5: while Array[Right] > pivot
Move Left
Step 6: If no match found in step 5 and step 6, swap Left and Right
Step 7: If Left ≥ Right, their meeting point is the new pivot

Quicksort Algorithm:

Step 1 − Array[Right] = pivot
Step 2 − Apply partition algorithm over data items using pivot element
Step 3 − quicksort(left of pivot)
Step 4 − quicksort(right of pivot)

Quick Sort Partition Pseudo-code:

procedure Partition (Array[], low, high):
    pivot = Array[high]  
    i = low-1  
    for (j = low; j <= high- 1; j++):
        if (Array[j] < pivot):
            i++   
            swap (Array[i], Array[j])
        END if
    END for
    swap (Array[i+1], Array[high])
    return (i + 1)
END Partition

Quicksort Pseudo-code:

Quick_sort(Array[], low, high):
    if (low < high):
        partition_index = partition(arr, low, high)
        Quick_sort(Array, low, partition_index - 1)  
        Quick_sort(Array, partition_index + 1, high)
    END if
END Quick_sort

Quicksort Implementation in C:

#include <stdio.h>

void swap(int* num1, int* num2)
{
  int temp = *num1;
  *num1 = *num2;
  *num2 = temp;
}

int Partition (int Array[], int low, int high)
{
  int pivot = Array[high]; 
  int i = low - 1; 
  for (int j = low; j <= high - 1; j++)
  {
    if (Array[j] < pivot)
    {
      i++; 
      swap(&Array[i], &Array[j]);
    }
  }
  swap(&Array[i + 1], &Array[high]);
  return (i + 1);
}

void Quick_sort(int Array[], int low, int high)
{
  if (low < high)
  {
    int Partition_index = partition(arr, low, high);
    Quick_sort(Array, low, partition_index - 1);
    Quick_sort(Array, partition_index + 1, high);
  }
}

void Display_array(int arr[], int size)
{
  for (int i = 0; i < size; i++)
    printf("%d, arr[i]");
  printf("\n");
}

int main()
{
  int array[] = {8,7,3,6,5,2,4};
  int n = sizeof(array) / sizeof(array[0]);
  Quick_sort(array, 0, n - 1);
  printf("Sorted array is: ");
  Display_array(array, n);
  return 0;
}

Implementation of QuickSort in C++

#include <bits/stdc++.h>
using namespace std;

void swap(int* num1, int* num2)
{
  int temp = *num1;
  *num1 = *num2;
  *num2 = temp;
}

int Partition (int Array[], int low, int high)
{
  int pivot = Array[high]; 
  int i = low - 1; 
  for (int j = low; j <= high - 1; j++)
  {
    if (Array[j] < pivot)
    {
      i++; 
      swap(&Array[i], &Array[j]);
    }
  }
  swap(&Array[i + 1], &Array[high]);
  return (i + 1);
}

void Quick_sort(int Array[], int low, int high)
{
  if (low < high)
  {
    int Partition_index = partition(arr, low, high);
    Quick_sort(Array, low, partition_index - 1);
    Quick_sort(Array, partition_index + 1, high);
  }
}

void Display_array(int arr[], int size)
{
  for (int i = 0; i < size; i++)
    cout << arr[i];
  cout << endl;;
}

int main()
{
  int array[] = {8,7,3,6,5,2,4};
  int n = sizeof(array) / sizeof(array[0]);
  Quick_sort(array, 0, n - 1);
  cout << "Sorted array is: ";
  Display_array(array, n);
  return 0;
}

Implementation of Quicksort in Java:

import java.io.*;

class TechVidvan{

    static void swap(int[] Array, int i, int j)
    {
    	int temp = Array[i];
    	Array[i] = Array[j];
    	Array[j] = temp;
    }
    
    static int Partition(int[] Array, int low, int high)
    {
    	int pivot = Array[high];
    	int i = low - 1;
    
    	for(int j = low; j <= high - 1; j++)
    	{
    		if (Array[j] < pivot)
    		{
    			i++;
    			swap(Array, i, j);
    		}
    	}
    	swap(Array, i + 1, high);
    	return (i + 1);
    }
    
    static void Quick_sort(int[] Array, int low, int high)
    {
    	if (low < high)
    	{
    		int partition_index = Ppartition(arr, low, high);
    		Quick_sort(Array, low, partition_index - 1);
    		Quick_sort(Array, partition_index + 1, high);
    	}
    }
    
    static void Display_array(int[] arr, int size)
    {
    	for(int i = 0; i < size; i++)
    		System.out.print(arr[i] + " ");
    	System.out.println();
    }
    
    public static void main(String[] args)
    {
    	int[] array = {8,7,3,6,5,2,4};
    	int n = array.length;
    	Quick_sort(array, 0, n - 1);
    	System.out.println("Sorted array: ");
    	Display_array(array, n);
    }
}

Implementation of Quicksort in Python:

def Partition(low, high, Array):

  pivot_index = low
  pivot = Array[pivot_index]
  while low < high:
    while low < len(Array) and Array[low] <= pivot:
      start += 1
    while Array[high] > pivot:
      end -= 1
    if(low < high):
      Array[low], Array[high] = Array[high], Array[low]
  Array[high], Array[pivot_index] = Array[pivot_index], array[high]
  return high
  
def Quick_sort(low, highd, Array):
  
  if (low < high):
    p = Partition(low, high, Array)
    Quick_sort(low, p - 1, Array)
    Quick_sort(p + 1, high, Array)

list = [8,7,3,6,5,2,4]
Quick_sort(0, len(list) - 1, list)

print(f'Sorted array: {list}')

Complexity of Quicksort

In quicksort, we sort the array by dividing it into sub-problems.

We divide a problem of size ‘n’ into two subproblems of size k and (n-1-k). Thus, the recursive function for the time complexity is:
T(n) = T(k) + T(n-k-1) + θ(n)
Here, θ(n) is added because of the time taken by the partition process.

On solving this recursive equation, we will get the time complexity to be:

Scenario	Time complexity
Worst case	O(n2)
Average case	O(n logn)
Best case	O(n logn)

Also, quicksort is an in-place sorting algorithm.

3-Way Quicksort

We mostly used 3-way quicksort whenever we have redundant elements i.e. the same element is repeated more than once in the array. In the default version of quicksort, we choose a pivot point and divide the array based on the elements less than and greater than the pivot element respectively. But in 3-way quicksort, we divide the array into three sub-arrays instead of two sub-arrays.

• The first sub-array contains all the elements less than the pivot element.
• The second sub-array contains all the elements equal to the pivot element in case the pivot element is repeated.
• The third sub-array contains all the values greater than the pivot element.

For example, consider the following array: {1, 3, 5, 3, 6, 12, 4, 5, 3, 7, 12, 3, 18, 4, 22, 3}. In this array, we have three redundant elements: 3, 4, 12. So, we will use 3-way quicksort for this array. Suppose the array ranges from arr[l..r].

Then,

1. The first sub-array will be from arr[l..i] having values less than the pivot element.

2. The second sub-array will be from arr[i+1..j-1] having values equal to the pivot element.

3. The third sub-array will be from arr[j..r] having values greater than the pivot element.

Quicksort on Singly Linked List

Just like arrays, we can sort linked lists as well using a quicksort algorithm. We usually take the last element as the pivot element and bring it to its correct position in each iteration.

Singly Linked list Implementation of Quicksort in C

#include <stdio.h>
struct Node {
  int key;
  struct Node* Next;
};

void Push(struct Node** head_referrence, int new_key)
{
  struct Node* new_node = new Node;
  new_node-> key = new_key;
  new_node-> Next = (*head_referrence);
  (*head_referrence) = new_node;
}

void Display_list(struct Node* Node)
{
  while (Node != NULL) {
    printf("%d ", Node->key);
    Node = Node->Next;
  }
  printf("\n");
}

struct Node* get_tail(struct Node* current)
{
  while (current != NULL && current->Next != NULL)
    current = current->Next;
  return current;
}

struct Node* partition(struct Node* head, struct Node* end,
          struct Node** newHead,
          struct Node** newEnd)
{
  struct Node* pivot = end;
  struct Node *prev = NULL, *current = head, *tail = pivot;
  while (current != pivot) {
    if (current->data < pivot->data) {
      if ((*newHead) == NULL)
        (*newHead) = current;

      prev = current;
      current = current->next;
    }
    else 
    {
      if (prev)
        prev->Next = current->Next;
      struct Node* tmp = current->Next;
      current->Next = NULL;
      tail->Next = current;
      tail = current;
      current = tmp;
    }
  }
  if ((*newHead) == NULL)
    (*newHead) = pivot;
  (*newEnd) = tail;
  return pivot;
}

struct Node* quick_sort_rec(struct Node* head,
              struct Node* end)
{
  if (!head || head == end)
    return head;

  Node *newHead = NULL, *newEnd = NULL;
  struct Node* pivot
    = partition(head, end, &newHead, &newEnd);
  if (newHead != pivot) {
    struct Node* tmp = newHead;
    while (tmp->Next != pivot)
      tmp = tmp->Next;
    tmp->Next = NULL;
    newHead = quick_sort_rec(newHead, tmp);
    tmp = getTail(newHead);
    tmp->Next = pivot;
  }
  pivot->Next = quick_sort_rec(pivot->Next, newEnd);
  return newHead;
}

void quick_sort(struct Node** headRef)
{
  (*headRef)
    = quick_sort_rec(*headRef, getTail(*headRef));
  return;
}

int main()
{
  struct Node* a = NULL;
  push(&a, 12);
  push(&a, 20);
  push(&a, 15);
  push(&a, 5);
  push(&a, 21);

  printf("Linked List before sorting \n");
  Display_list(a);

  quick_sort(&a);

  printf( "Linked List after sorting \n");
  Display_list(a);
  return 0;
}

Singly Linked list Implementation of Quicksort in C++

#include <bits/stdc++.h>
using namespace std;

struct Node {
  int key;
  struct Node* Next;
};

void Push(struct Node** head_referrence, int new_key)
{
  struct Node* new_node = new Node;
  new_node-> key = new_key;
  new_node-> Next = (*head_referrence);
  (*head_referrence) = new_node;
}

void Display_list(struct Node* Node)
{
  while (Node != NULL) {
    cout << "%d ", Node->key;
    Node = Node->Next;
  }
  cout << endl;
}

struct Node* get_tail(struct Node* current)
{
  while (current != NULL && current->Next != NULL)
    current = current->Next;
  return current;
}

struct Node* partition(struct Node* head, struct Node* end,
          struct Node** newHead,
          struct Node** newEnd)
{
  struct Node* pivot = end;
  struct Node *prev = NULL, *current = head, *tail = pivot;
  while (current != pivot) {
    if (current->data < pivot->data) {
      if ((*newHead) == NULL)
        (*newHead) = current;

      prev = current;
      current = current->next;
    }
    else 
    {
      if (prev)
        prev->Next = current->Next;
      struct Node* tmp = current->Next;
      current->Next = NULL;
      tail->Next = current;
      tail = current;
      current = tmp;
    }
  }
  if ((*newHead) == NULL)
    (*newHead) = pivot;
  (*newEnd) = tail;
  return pivot;
}

struct Node* quick_sort_rec(struct Node* head,
              struct Node* end)
{
  if (!head || head == end)
    return head;

  Node *newHead = NULL, *newEnd = NULL;
  struct Node* pivot
    = partition(head, end, &newHead, &newEnd);
  if (newHead != pivot) {
    struct Node* tmp = newHead;
    while (tmp->Next != pivot)
      tmp = tmp->Next;
    tmp->Next = NULL;
    newHead = quick_sort_rec(newHead, tmp);
    tmp = getTail(newHead);
    tmp->Next = pivot;
  }
  pivot->Next = quick_sort_rec(pivot->Next, newEnd);
  return newHead;
}

void quick_sort(struct Node** headRef)
{
  (*headRef)
    = quick_sort_rec(*headRef, getTail(*headRef));
  return;
}

int main()
{
  struct Node* a = NULL;
  push(&a, 12);
  push(&a, 20);
  push(&a, 15);
  push(&a, 5);
  push(&a, 21);

  cout << "Linked List before sorting \n";
  Display_list(a);

  quick_sort(&a);

  cout << "Linked List after sorting \n";
  Display_list(a);
  return 0;
}

Implementation of Singly Linked list Quicksort in Java:

public class Quicksort_linkedlist {
  static class Node {
    int key;
    Node Next;

    Node(int d)
    {
      this.key = d;
      this.Next = null;
    }
  }

  Node head;

  void add_node(int key)
  {
    if (head == null) {
      head = new Node(key);
      return;
    }
    Node current = head;
    while (current.Next != null)
      current = current.Next;
    Node newNode = new Node(key);
    current.next = newNode;
  }

  void Display_list(Node n)
  {
    while (n != null) {
      System.out.print(n.key);
      System.out.print(" ");
      n = n.Next;
    }
  }
  Node parition(Node start, Node end)
  {
    if (start == end || start == null || end == null)
      return start;

    Node pivot_prev = start;
    Node current = start;
    int pivot = end.key;
    while (start != end) {
      if (start.key < pivot) {
        pivot_prev = current;
        int temp = current.key;
        current.key = start.key;
        start.key = temp;
        current = current.Next;
      }
      start = start.Next;
    }

    int temp = current.key;
    current.key = pivot;
    end.key = temp;
    return pivot_prev;
  }

  void quick_sort(Node start, Node end)
  {
    if(start == null || start == end|| start == end.Next )
      return;
    Node pivot_prev = parition(start, end);
    quick_sort(start, pivot_prev);
    if (pivot_prev != null && pivot_prev == start)
      quick_sort(pivot_prev.Next, end);
    else if (pivot_prev != null	&& pivot_prev.next != null)
      quick_sort(pivot_prev.Next.Next, end);
  }

public static void main(String[] args)
  {
    Quicksort_linkedlist list = new Quicksort_linkedlist();
    list.addNode(12);
    list.addNode(20);
    list.addNode(15);
    list.addNode(5);
    list.addNode(21);

    Node n = list.head;
    while (n.Next != null)
      n = n.Next;

    System.out.println("Linked List before sorting");
    list.Display_list(list.head);

    list.quick_sort(list.head, n);

    System.out.println("\nLinked List after sorting");
    list.Display_list(list.head);
  }
}

Singly Linked list Implementation of Quicksort in Python:

class Node:
  def __init__(self, val):
    self.data = key
    self.Next = None

class Quicksort_linkedlist:
  def __init__(self):
    self.head=None
  def addNode(self,data):
    if (self.head == None):
      self.head = Node(data)
      return
    current = self.head
    while (current.Next != None):
      current = current.Next
    newNode = Node(data)
    current.Next = newNode

  def Display_list(self,n):
    while (n != None):
      print(n.data, end=" ")
      n = n.Next

  def parition(self,start, end):
    if (start == end or start == None or end == None):
      return start
    pivot_prev = start
    current = start
    pivot = end.data
    while (start != end):
      if (start.data < pivot):
        pivot_prev = current
        temp = current.data
        curr.data = start.data
        start.data = temp
        current = current.Next
      start = start.Next
    temp = current.data
    current.data = pivot
    end.data = temp
    return pivot_prev

  def quick_sort(self, start, end):
    if(start == None or start == end or start == end.Next):
      return
    pivot_prev = self.parition(start, end)
    self.quick_sort(start, pivot_prev)
    if(pivot_prev != None and pivot_prev == start):
      self.quick_sort(pivot_prev.Next, end)
    elif (pivot_prev != None and pivot_prev.Next != None):
      self.quick_sort(pivot_prev.Next.Next, end)

if __name__ == "__main__":
  ll = Quicksort_linkedlist()
  ll.addNode(12)
  ll.addNode(20)
  ll.addNode(15)
  ll.addNode(5)
  ll.addNode(21)

  n = ll.head
  while (n.Next != None):
    n = n.next

  print("\nLinked List before sorting")
  ll.Display_list(ll.head)

  ll.quick_sort(ll.head, n)

  print("\nLinked List after sorting");
  ll.Display_list(ll.head)

Doubly Linked list Implementation of Quicksort in C:

#include <stdio.h>
#include <stdlib.h>

struct Node
{
  int key;
  struct Node *Next;
  struct Node *Prev;
};

void swap ( int* a, int* b )
{ 
    int t = *a; 
    *a = *b; 
    *b = t; 
}

struct Node *lastNode(struct Node *root)
{
  while (root && root->Next)
    root = root->Next;
  return root;
}

struct Node* partition(struct Node *l, struct Node *h)
{
  int x = h->key;
  struct Node *i = l->Prev;
  for (struct Node *j = l; j != h; j = j->Next)
  {
    if (j->key <= x)
    {
      i = (i == NULL) ? l : i->Next;
      swap(&(i->key), &(j->key));
    }
  }
  i = (i == NULL) ? l : i->Next; 
  swap(&(i->key), &(h->key));
  return i;
}

void quick_sort(struct Node* l, struct Node *h)
{
  if (h != NULL && l != h && l != h->Next)
  {
    struct Node *p = partition(l, h);
    quick_sort(l, p->Prev);
    quick_sort(p->Next, h);
  }
}

void quick_sort(struct Node *head)
{
  struct Node *h = lastNode(head);
  quick_sort(head, h);
}

void Display_list(struct Node *head)
{
  while (head)
  {
    printf("%d ", head->key);
    head = head->Next;
  }
  printf("\n");
}

void push(struct Node** head_ref, int new_key)
{
  struct Node* new_node = (struct Node*) malloc(sizeof(struct Node)); 
  new_node->key = new_key;
  new_node->Prev = NULL;
  new_node->Next = (*head_ref);
  if ((*head_ref) != NULL) (*head_ref)->Prev = new_node ;
  (*head_ref) = new_node;
}

int main(int argc, char **argv)
{
  struct Node *a = NULL;
  push(&a, 12);
  push(&a, 20);
  push(&a, 15);
  push(&a, 5);
  push(&a, 21);

  printf("Linked List before sorting \n");
  Display_list(a);
  quick_sort(a);
  printf("Linked List after sorting \n");
  Display_list(a);
  return 0;
}

Implementation of Doubly Linked list Quicksort in C++

#include <bits/stdc++.h>
using namespace std;

struct Node
{
  int key;
  struct Node *Next;
  struct Node *Prev;
};

void swap ( int* a, int* b )
{ 
    int t = *a; 
    *a = *b; 
    *b = t; 
}

struct Node *lastNode(struct Node *root)
{
  while (root && root->Next)
    root = root->Next;
  return root;
}

struct Node* partition(struct Node *l, struct Node *h)
{
  int x = h->key;
  struct Node *i = l->Prev;
  for (struct Node *j = l; j != h; j = j->Next)
  {
    if (j->key <= x)
    {
      i = (i == NULL) ? l : i->Next;
      swap(&(i->key), &(j->key));
    }
  }
  i = (i == NULL) ? l : i->Next; 
  swap(&(i->key), &(h->key));
  return i;
}

void quick_sort(struct Node* l, struct Node *h)
{
  if (h != NULL && l != h && l != h->Next)
  {
    struct Node *p = partition(l, h);
    quick_sort(l, p->Prev);
    quick_sort(p->Next, h);
  }
}

void quick_sort(struct Node *head)
{
  struct Node *h = lastNode(head);
  quick_sort(head, h);
}

void Display_list(struct Node *head)
{
  while (head)
  {
    cout << "%d ", head->key;
    head = head->Next;
  }
  cout << endl;
}

void push(struct Node** head_ref, int new_key)
{
  struct Node* new_node = (struct Node*) malloc(sizeof(struct Node)); 
  new_node->key = new_key;
  new_node->Prev = NULL;
  new_node->Next = (*head_ref);
  if ((*head_ref) != NULL) (*head_ref)->Prev = new_node ;
  (*head_ref) = new_node;
}

int main(int argc, char **argv)
{
  struct Node *a = NULL;
  push(&a, 12);
  push(&a, 20);
  push(&a, 15);
  push(&a, 5);
  push(&a, 21);

  cout <<"Linked List before sorting \n";
  Display_list(a);
  quick_sort(a);
  cout <<"Linked List after sorting \n";
  Display_list(a);
  return 0;
}

Doubly Linked list Implementation of Quicksort in Java:

class Quicksort_doublylinkedlist{
  Node head;
  static class Node{
    private int Key;
    private Node Next;
    private Node Prev;
    Node(int d){
      Key = d;
      Next = null;
      Prev = null;
    }
  }
  
  Node lastNode(Node node){
    while(node.Next!=null)
      node = node.Next;
    return node;
  }

  Node partition(Node l,Node h)
  {
    int x = h.Key;
    Node i = l.Prev;
    for(Node j=l; j!=h; j=j.Next)
    {
      if(j.Key <= x)
      {
        i = (i==null) ? l : i.Next;
        int temp = i.Key;
        i.Key = j.Key;
        j.Key = temp;
      }
    }
    i = (i==null) ? l : i.Next; 
    int temp = i.Key;
    i.Key = h.Key;
    h.Key = temp;
    return i;
  }
  
  void quick_sort(Node l,Node h)
  {
    if(h!=null && l!=h && l!=h.Next){
      Node temp = partition(l,h);
      quick_sort(l,temp.Prev);
      quick_sort(temp.Next,h);
    }
  }
  
  public void quickSort(Node node)
  {
    Node head = lastNode(node);
    quick_sort(node,head);
  }
  
  public void Display_list(Node head)
  {
    while(head!=null){
      System.out.print(head.Key + " ");
      head = head.Next;
    }
  }
  
  void push(int new_key)
  {
    Node new_Node = new Node(new_key);	 
    if(head==null){
      head = new_Node;
      return;
    }
    new_Node.Next = head;
    head.Prev = new_Node;
    new_Node.Prev = null;
    head = new_Node;
  }
  
  public static void main(String[] args){
      Quicksort_doublylinkedlist list = new Quicksort_doublylinkedlist();
      list.push(12);
      list.push(20);
      list.push(15);
      list.push(5);
      list.push(21);
      System.out.println("Linked List before sorting ");
      list.Display_list(list.head);
      System.out.println("\nLinked List after sorting");
      list.quickSort(list.head);
      list.Display_list(list.head);
  }
}

Difference between Merge Sort and Quicksort:

Merge sort	Quicksort
It takes extra memory of O(n), therefore it is not inplace.	Quicksort is an inplace sorting technique.
The default implementation of merge sort is stable.	Quick sort’s default implementation is not stable.
For linked lists, we prefer merge sort over quicksort.	For sorting of arrays, we prefer quicksort over merge sort.
Merge sort does not follow tail recursion property.	Quicksort is a tail-recursive algorithm.
Merge sort does not allow random accessing of elements.	Quicksort allows random access.

Advantages of Quicksort

1. It doesn’t occupy extra space.
2. It provides cache friendliness, as it has a good locality of reference.
3. It performs tail recursion elimination which makes it even more efficient.
4. It has less time and space complexity.

Applications of Quicksort

1. Quicksort is used to implement primitive type methods.
2. It is commercially used for sorting because it is one of the fastest sorting techniques.
3. Quicksort provides cache friendliness.
4. Quicksort works well in event-driven simulations.
5. Quicksort is implemented through a priority queue and most of the efficiently developed algorithms also use a priority queue. Thus, making use of quick sort becomes easier.

Conclusion

Quicksort is one of the most efficient and widely used sorting techniques. It is called ‘quick’ because it provides cache friendliness and tail recursion optimization.

In this article, we have covered the working, implementation and advantages of quicksort. We have also seen how it is different from merge sort.