Stack in Data Structure
Every data structure either has an Abstract view or a concrete view. In an abstract view, we hide the implementation details. In concrete view, there is an actual implementation of the data structure.
A stack follows an abstract view. Thus, the stack is an Abstract Data Type(ADT). Stack data structure behaves exactly like a real-life stack. Eg: A pile/stack of books.
What is a Stack?
A stack is a linear data structure. It works on LIFO(Last in first out) or FILO(First in last out) approach. A stack contains a pointer named ‘top’. This pointer points to the top of the stack.
In stack, we can perform insertion and deletion operations at only one end i.e. at the top of the stack.
Stack as an ADT
Stack is an abstract data type i.e. ADT. It has a pre-defined capacity. That is why it can store only a limited number of values. It follows the LIFO approach.
Order of deletion of elements is the reverse of the order of insertion. Insertion and deletion are performed at only one end. That end is called ‘top’.
Stack is also known as restricted data structure because insertion and deletion operations can be performed at only one end.
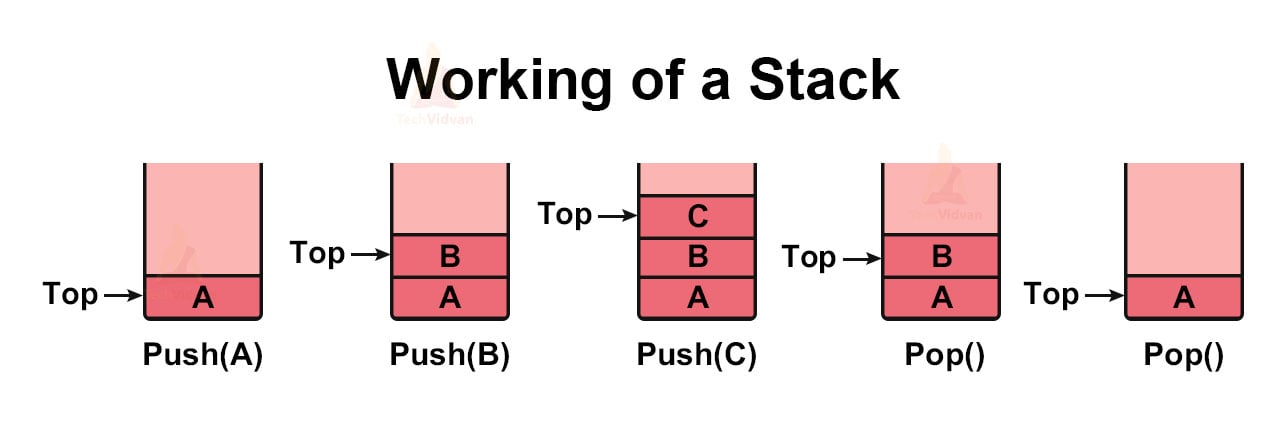
Working of a Stack in Data Structure
In stack, the elements that enter the last come out the first. Let us understand the working of a stack with the help of an example.
Consider that the stack is initially empty. When we insert ‘A’ into it, the ‘top’ pointer starts pointing to A. we will insert the next element above A. When we insert ‘B’ above A, the pointer ‘top’ points to B. In this manner, all the elements are pushed into the stack. Finally, ‘top’ will point to the uppermost element in the stack.
The following diagram shows the working of the stack:
If we wish to remove the elements, we will use the pop( ) operation. We can remove elements only from the top of the stack. If we pop C and D, the final elements in the stack will be A, B.
Operations defined on Stack:
1. Push( ): Inserting an element is defined as Push( ) operation in stack.
2. Popl( ): This operation deletes elements from the stack.
3. IsEmpty( ): It checks whether the stack is empty or not. It returns either true or false.
4. IsFull( ): It checks whether the stack is full or not. IsFull( ) is checked only during actual implementation.
5. peep( ): This operation gives the value of the top data element of the stack without removing it.
6. count( ): It is used to count the number of elements in the stack.
7. change( ): This operation is used to change the element at the given position.
8. display( ): It displays/prints the elements of the stack.
Let us see these operations in detail now:
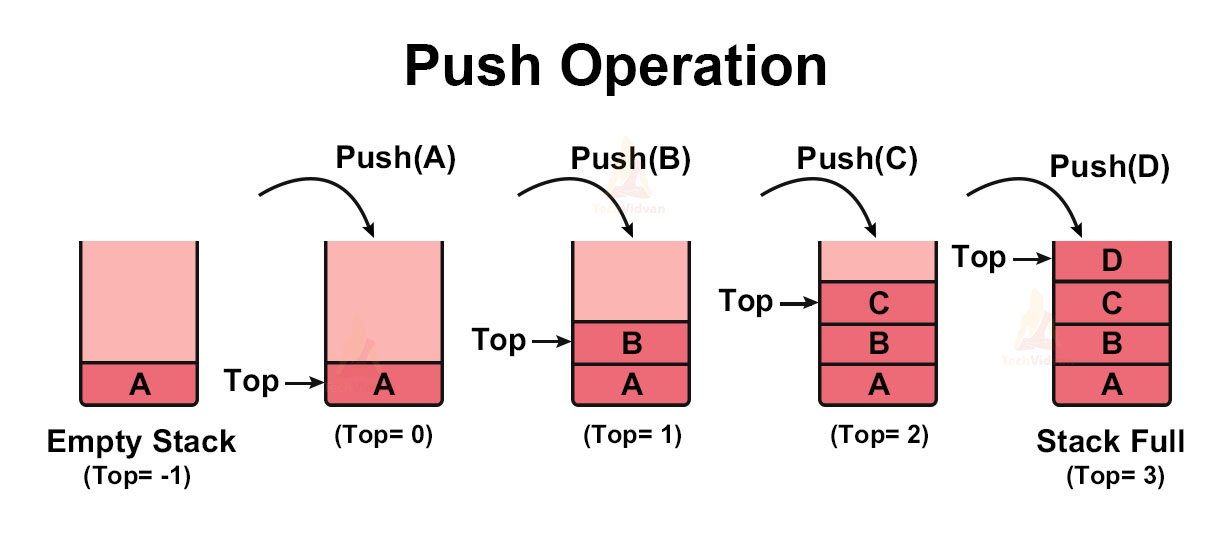
1. Push Operation in Stack
Through this operation, we add new elements to our stack. The push( ) operation goes through the following steps:
1. Before inserting a new element into the stack, check whether the stack is full or not.
2. If the stack is already full and we try to insert more elements into it, it will return an overflow error.
3. If the stack is not full, increment the ‘top’ to point to the next empty space and insert the new element there.
4. When the stack is empty, ‘top’ points to -1. Once we add a new element, the ‘top’ points to that element and has a value of 0.
5. The stack can accommodate elements as long as it does not reach its maximum capacity.
Push operation is shown diagrammatically as follows:
Algorithm for Push( ) operation:
void push_into_stack(int key)
{
if(top == SIZE-1) //When stack is full //Here, SIZE is the total stack capacity
{
print("Overflow");
return;
}
top = top+1; //Incrementing top by 1
stack[top] = key; //Inserting the element
}
Example of Push Operation in Stack
void PUSH(int key) {
if(!isFull()) {
top = top+1;
Stack[top] = key;
} else {
printf("Stack is already full.\n");
}
}
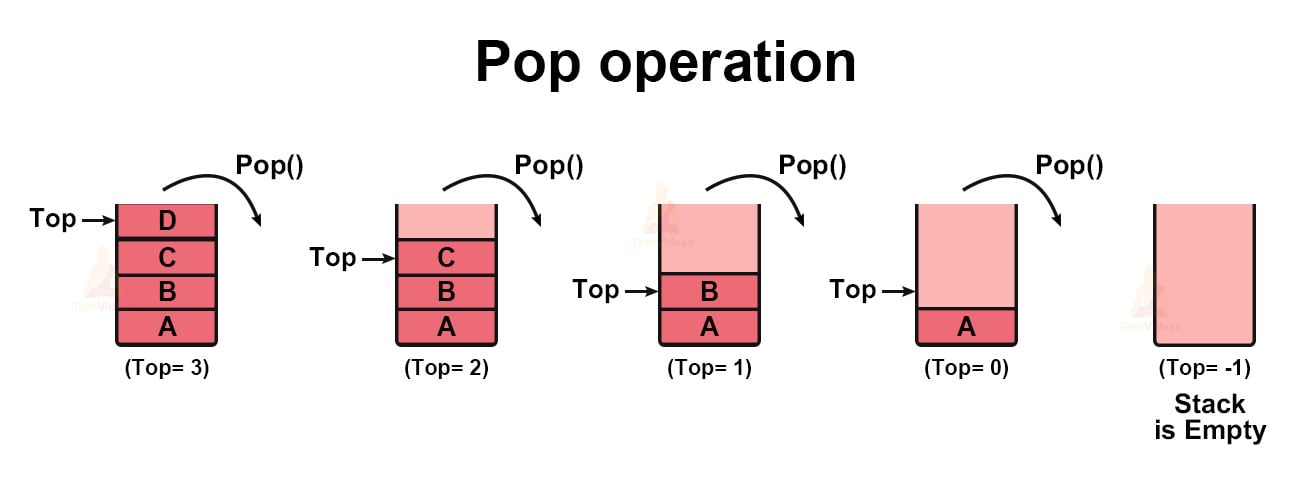
2. Pop Operation in Stack
It helps in removing elements from the top of the stack. The steps involved in the pop operation are:
1. The first step is to check whether the stack is empty or not.
2. If the stack is already empty, we cannot remove any element from it. So, we will return an underflow error.
3. If the stack is not empty, remove the topmost element of the stack.
4. Decrement the position of ‘top’ by 1 and return.
The following example explains the pop operation:
In the pop( ) operation, we need not specify the element to be removed, because the pop operation can only delete the uppermost element.
Pseudo-code for the pop( ) operation
int pop()
{
int temp; //To store the element to be deleted
if(top == -1) //If stack is empty
{
print("Overflow");
break;
}
temp = stack[top];
top = top-1;
return temp;
}
Example of Pop() Operation in Stack
int POP(int key)
{
if(!isempty()) {
key = Stack[top];
top = top-1;
return key;
}
else {
printf("No data found, Stack is already empty.\n");
}
}
3. peek( ) Operation in Stack
This operation prints the topmost element of the stack.
Pseudo-code for Stack Peek() Operation
int peek()
{
return stack[top]; //prints the value to which the 'top' points
}
Example of Peek() Operation in Stack
int peek() {
return Stack[top];
}
4. IsFull( ) and IsEMpty( ) Operations in Stack
IsFull( ) returns TRUE if the stack is full, else it returns FALSE.
IsEmpty( ) is the opposite of IsFull( ) operation. It returns TRUE if the stack is empty. Otherwise, it will return FALSE.
Pseudo-code of IsFull() and IsEmpty() in Stack
bool IsFull() {
if(top == SIZE-1) //Here, SIZE is the total stack capacity
return true;
else
return false;
}
bool IsEmpty() {
if(top == -1)
return true;
else
return false;
}
Example of isFull() in Stack
bool isfull() {
if(top == SIZE)
return true;
else
return false;
}
Example of Stack isempty():
bool isempty() {
if(top == -1)
return true;
else
return false;
}
Implementation of Stack in Data Structure
The stack can be implemented mainly with the help of two data structures:
- Using arrays
- Using linked lists.
Let us discuss both of them in detail.
1. Array implementation of Stack:
When we implement a stack using a particular data structure, its advantages and disadvantages will become the advantages and disadvantages of the stack as well.
In array implementation, we perform all the operations using arrays. Therefore, the properties of arrays become the properties of the stack as well.
For example, an advantage of the array is the ability of random access. If we implement a stack using an array, this becomes the advantage of the stack as well.
A disadvantage of an array is the preallocation of memory. Thus, this becomes the disadvantage of the stack as well.
a. Push Operation using Arrays:
In a push operation, we add an element at the top of the stack and then increment the position of the top by 1. If the stack is already full, it will return an overflow error and the program will terminate.
The C implementation of push() operation is given as follows:
{
if (top == SIZE-1)
printf("Overflow, Stack is already full");
else
{
top = top+1;
Stack[top] = key;
}
}
The time complexity of the above code is O(1).
b. Pop Operation using Arrays:
It involves deleting an element from the top of the stack. It returns an underflow error if the stack is already empty.
The C implementation of pop operation is given below.
int pop () //The return type of this function is int because at the end we need to return the deleted element
{
if(top == -1) //-1 signifies invalid address
{
printf("Underflow, Stack is already empty");
break;
}
else
{
Stack[top] = Stack[top]-1;
return Stack[top];
}
}
The time complexity to perform the pop operation using arrays is O(1).
c. Peek Operation using Arrays:
It displays the topmost element without deleting it. The implementation of peek operation in C language is as follows:
int peek()
{
if (top == -1)
{
printf("The stack is already empty");
break;
}
return stack [top];
}
The time taken by this code is constant i.e. O(1).
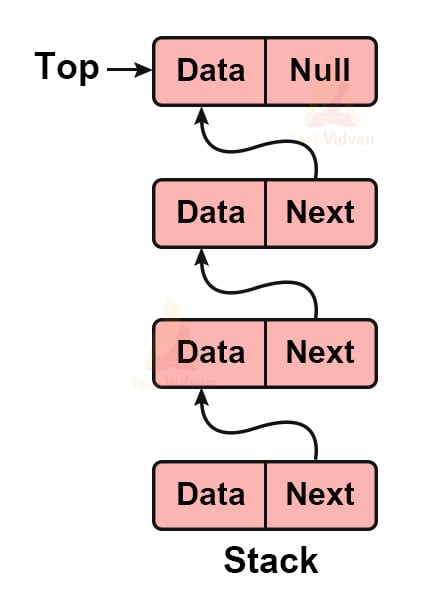
2. Linked List implementation of Stack:
- Another way to implement a stack is using linked lists.
- The linked list allocates memory dynamically. Thus, the stack will also have dynamic memory allocation.
- Since there is dynamic memory allocation, the use of heap comes into the picture.
- In the case of the linked list implementation, the stack will be considered full if the heap does not have enough space to create a new node.
- In a linked list, the last node points to NULL. if the stack is implemented using a linked list, its topmost node will point to NULL as well.
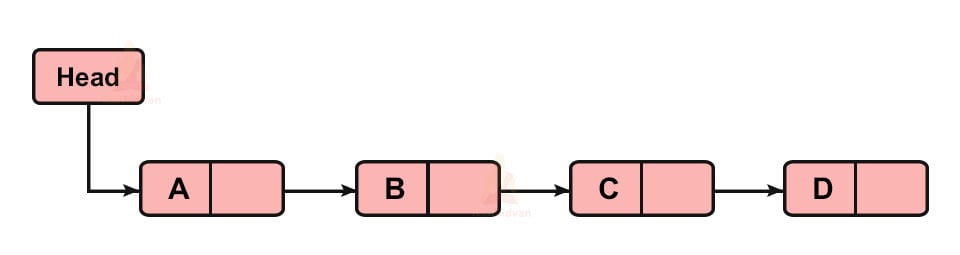
The linked list representation of the stack is shown below:
a. Push Operation using Linked List:
- Using the push() operation, we can add a new node into the stack.
- The first step is to create a node and allocate memory to it.
- Next, we need to check the number of nodes already present in the list.
- If the list is empty, insert the node. Assign the value to the data section of the node and assign NULL to the link section of the node.
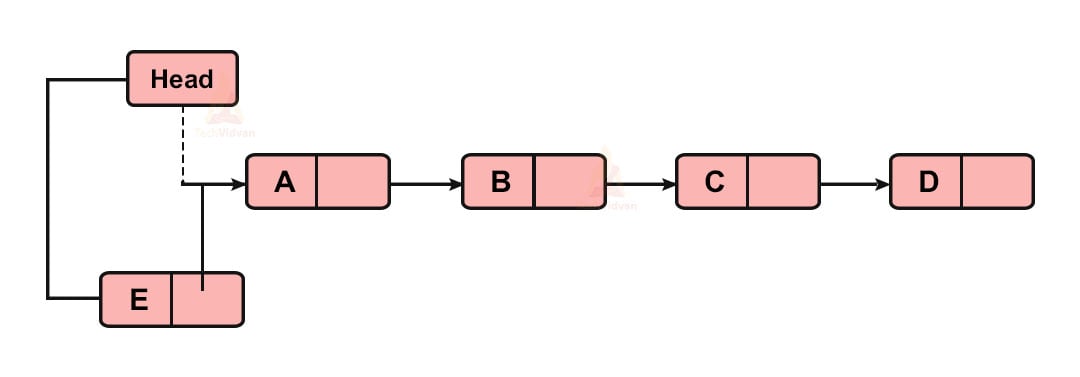
- If the list has one or more nodes already, insert the new node in the beginning so as to preserve the properties of the stack.
For example, suppose we have a stack with value A, B, C, D as shown:
Since the stack already has a few nodes, the new node will insert at the beginning.
The time complexity of the push operation is of constant order i.e. O(1).
The implementation of stack using linked list is C is shown below:
void push (int key)
{
struct Node *Ptr =(struct Node*)malloc(sizeof(struct Node));
if(Ptr == NULL)
{
printf("New vale can't be inserted");
}
else
{
printf("Enter the value");
scanf("%d",&key);
if(Head==NULL)
{
Ptr->key = key;
Ptr->Next = NULL;
Head = Ptr;
}
else
{
Ptr->key = key;
Ptr->Next = Head;
Head = Ptr;
}
printf("push() operation successfully executed");
}
}
b. Pop Operation using Linked List:
If the list is already empty, return an underflow error. In a stack, the pop operation can be performed at only one end. Thus, we will pop the first element of the list and adjust other pointers.
The code for the pop operation is given below:
void pop()
{
int key;
struct Node *Ptr;
if (Head == NULL)
printf("Stack is empty");
else
{
key = Head->data;
Ptr = Head;
Head = Head->Next;
free(Ptr);
printf("pop() Operation successful!");
}
}
The time complexity of the above code is O(n).
c. Displaying the nodes of the stack:
To display the nodes, we need to traverse the linked list and print each node.
To perform the display operation, create a temporary pointer named ‘temp’. Copy the Head pointer into temp. Traverse the list using this temporary pointer and print the values along the way.
The C implementation of the traverse and display operation is shown below:
void display()
{
int i;
struct node *temp;
temp = Head;
if(temp == NULL)
{
printf("Stack is empty");
}
else
{
printf("the elements in the Stack are \n");
while(tempmp != NULL)
{
printf("%d",temp->data);
temp = temp->next;
}
}
}
The time complexity of the display operation is of the order O(n).
Applications of Stack
1. Recursion
Recursion is one of the most basic but important applications of stack. It occurs when a function calls itself. We can use various algorithmic problems using recursion, such as Tower of Hanoi, Backtracking, Dynamic programming, Divide and conquer and many more.
Recursion makes use of the stack for implementation. Thus, stack in turn is helpful in solving all the above algorithmic computations.
2.Balancing of symbols
Stack is helpful in balancing pair symbols such as opening and closing braces, etc. Every program has a pair of opening and closing braces and shown:
int main()
{
printf("TechVidvan");
return 0;
}
Stack helps to balance these symbols so that at the end no symbol is left. Whenever an opening brace comes, we push it into the stack.
When the closing brace comes, we pop the closing brace out of the stack such that the stack becomes empty. At the end of the program, if any symbol still remains in the stack, it means that there is some syntactical error in the program.
3. Memory management
Stack is a part of main memory and it helps in memory management. Whenever we declare a variable inside a program, it is assigned to the stack memory and remains there until the program resides in the main memory.
Once the program executes, the stack memory releases all the variables.
4. Depth-first search
Depth-first search is a way of traversing elements inside the graph. This search/traversal technique makes use of graphs.
Graphs in turn use stack for implementation.
5. Backtracking
Whenever we need to backtrack through a problem, we make use of stack data structure. Backtracking involves recursion and recursion involves the usage of the stack.
6. String reversal
Stack helps to reverse a string.
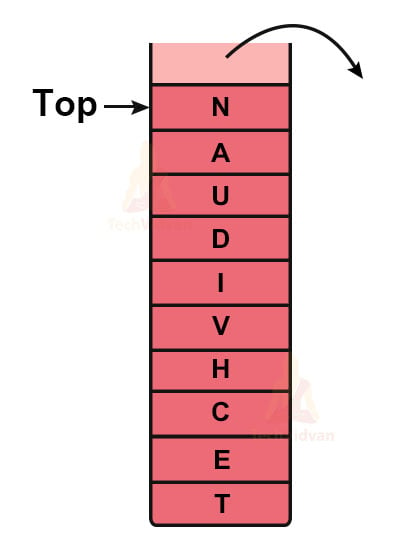
Suppose we wish to reverse the string- ‘TECHVIDVAN’. The stack reversal works as follows:
Here, the elements were pushed in the order: T→E→C→H→V→I→D→V→A→N.
But while popping, the elements will come out in reverse order i.e. N→A→V→D→I→V→H→C→E→T.
7. Expression conversion in Stack
Expression conversion is one of the most important applications of stack.
The expression conversions could be:
- Infix to prefix
- Infix to postfix
- Prefix to infix
- Prefix to postfix
- Postfix to infix
8. Undo/Redo:
Stack helps in performing undo and redo operations. There are two separate stacks maintained for undo and redo operations.
Suppose we want to write the string ‘STACK’, we will first write S, then T and so on. Thus, the states stored in the memory will be S, ST, STA, STAC, STACK.
We can perform undo and redo operations on these substrings using a stack.
Conclusion
Stack is one of the most important data structure in computer programming. It has a vast variety of applications as we have seen above.
In this article, we have seen various application areas of the stack, its use cases, and how to implement using pseudo-codes.