Tower of Hanoi in Data Structure

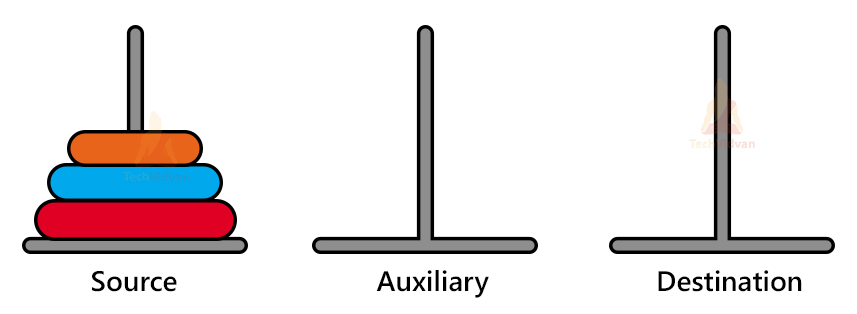
The Tower of Hanoi is a mathematical puzzle containing 3 pillars/towers with n disks each of a different size/diameter. These disks can slide onto any pillar. The following diagram shows the initial state of the problem.

Here, we have stacked the disks over each other in the ascending order of their sizes. Note that we can have any number of disks but only 3 towers.

Rules to be followed:

Our objective in this puzzle is to move all these disks to another pillar without changing the order in which the disks are placed in the initial state. The rules for this puzzle are:

1. We can move only one disk at a time.

2. We can remove only the top disk.

3. We can only place a disk above a disk of a larger size.

Approach:

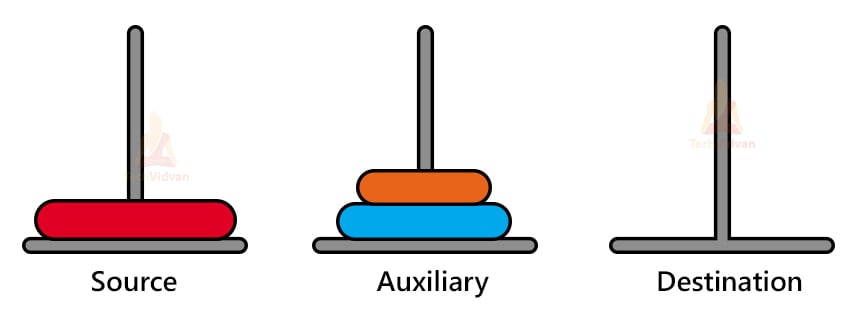
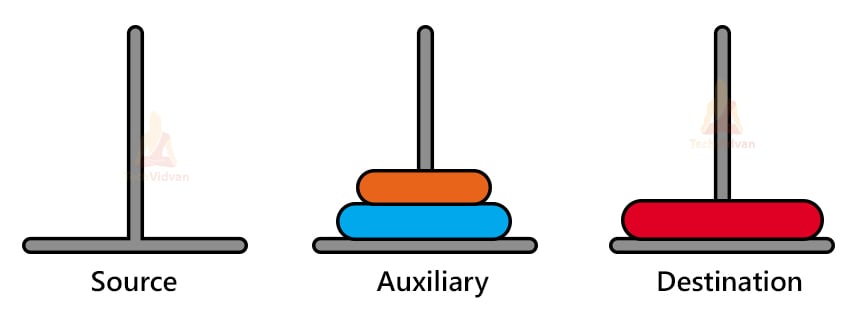
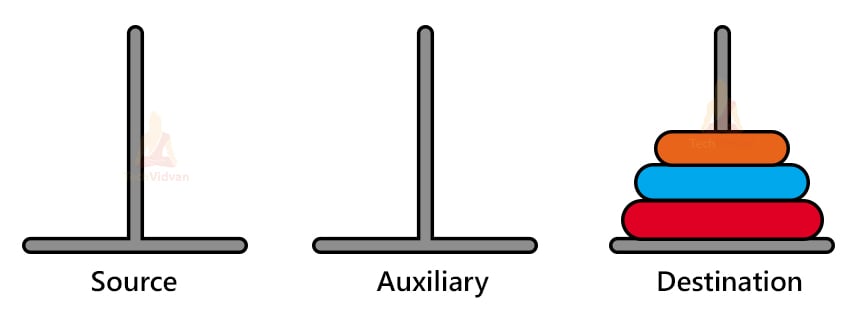
Tower of Hanoi is a recursion based puzzle and thus, we will follow a recursive approach to solve it. Consider a puzzle with 3 pillars and 3 disks as shown:

Step 1: toh(2, source, aux, dest)

Step 2: Move the disk from source to destination

Step 3: toh(2, aux, dest, source)

Thus, in general, for n disks, the steps are:

1: Move n-1 disks from source to auxiliary i.e. toh(n-1, source, aux, dest)
2: Move the nth disk from source to destination
3: Move n-1 disks from aux to dest i.e. toh(n-1, aux, dest, source)

Algorithm:

We can write the solution for this puzzle in both iterative and recursive approaches. Let us here see the steps to write a recursive algorithm for the Tower of Hanoi.

procedure TOH(disk, Source, Dest, Aux):
   if disk == 1:
        move disk from Source to Dest             
   else:
        TOH(disk - 1, Source, Aux, Dest)     
        move disk from Source to Dest          
        TOH(disk - 1, Aux, Dest, Source)     
   END if
END TOH

Implementation of Tower of Hanoi in C:

#include<stdio.h>
void toh(int, char, char, char);

int main(){
  char source = 'A', destination='B', Auxiliary='C';
  int n;
  printf("Enter value of n\t");
  scanf("%d", &n);
  toh(n, source, destination, Auxiliary);
  return 0;
}

void toh(int n, char source, char dest, char aux){
  if(n==1){
    printf("%c -> %c \n", source, dest);
    return;
  }
  toh(n-1, source, aux, dest);
  printf("%c -> %c \n", source, dest);
  toh(n-1, aux, dest, source);
}

Tower of Hanoi Implementation in C++:

#include<bits/stdc++.h>
void toh(int, char, char, char);

int main(){
  char source = 'A', destination='B', Auxiliary='C';
  int n;
  cout<< "Enter value of n\t";
  cin>> n;
  toh(n, source, destination, Auxiliary);
  return 0;
}

void toh(int n, char source, char dest, char aux){
  if(n==1){
    cout<< "%c -> %c \n"<< source<< dest;
    return;
  }
  toh(n-1, source, aux, dest);
  cout<< "%c -> %c \n"<< source<< dest;
  toh(n-1, aux, dest, source);
}

Implementation of Tower of Hanoi in Java:

import java.util.*;
import java.io.*;
import java.math.*;
class TechVidvan
{
static void toh(int n, char source, char dest, char aux)
{
  if (n == 1)
  {
    System.out.println("Move disk 1 from rod "+ source +" to rod "+ dest);
    return;
  }
  toh(n - 1, source, aux, dest);
  System.out.println("Move disk "+ n + " from rod " + source +" to rod " + dest );
  toh(n - 1, aux, dest, source);
}

public static void main(String args[])
{
  int n = 6; 
  toh(n, 'A', 'C', 'B'); 
}
}

Tower of Hanoi Implementation in Python:

def toh(n , source, dest, aux):
  if n == 1:
    print("Move disk 1 from tower",source,"to tower",dest)
    return
  toh(n-1, source, aux, dest)
  print("Move disk",n,"from rod",source,"to rod",dest)
  toh(n-1, aux, dest, source)

n = 6
toh(n, 'A', 'C', 'B')

Conclusion:

The puzzle Tower of Hanoi is like a mathematical disk game that was invented in 1883. We can play this puzzle with 3 towers/pillars and any number of disks. The solution for this puzzle is recursive. In this article, we have seen the recursive solution for Tower of Hanoi along with the rules of the puzzle.