Tree Traversal in Data Structure
Tree traversal means visiting each node of the tree. The tree is a non-linear data structure, and therefore its traversal is different from other linear data structures. There is only one way to visit each node/element in linear data structures, i.e. starting from the first value and traversing in a linear order. However, in tree data structures, there are multiple ways to traverse it.
Types of Tree Traversal:
Broadly, tree traversal is classified into two categories: Level order or breadth-first traversal and depth-first traversal. The depth-first traversal further has 3 different categories that we are going to study in detail.
Level Order Traversal:
In a level order traversal, the nodes are covered in a level-wise manner from left to right. We can implement a level order traversal with the help of a queue data structure.
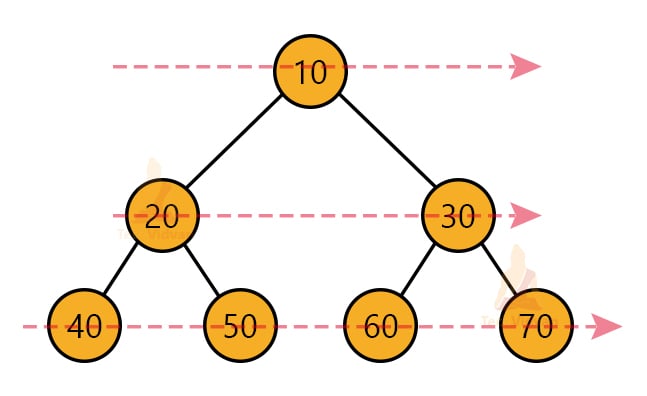
For example, the following diagram depicts the order of traversing the nodes of the tree.
Here, the level order traversal will print the nodes in the following order: 10, 20, 30, 40, 50, 60, 70.
Depth First Traversal:
In depth-first traversal, we go in one direction up to the bottom first and then come back and go to the other direction. There are three types of depth-first traversals. These are:
1. Preorder traversal
2. Inorder traversal
3. Postorder traversal
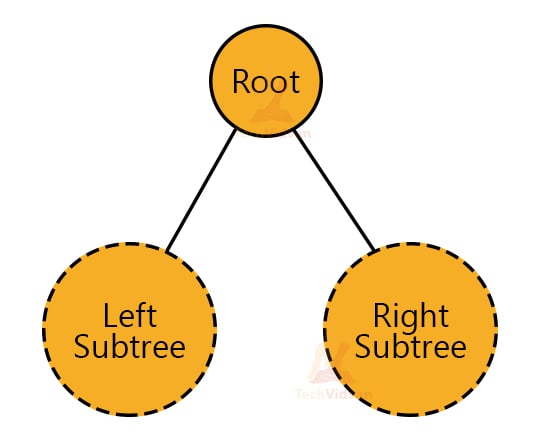
A binary tree is a recursive data structure. Also, each binary tree has 3 parts: a root node, a left subtree and a right subtree. These left and right subtrees are also trees in themselves and thus, again further described recursively.
A tree comprises multiple nodes. The structure of one node is:
struct Node {
int key;
struct Node* left;
struct Node* right;
}
Thus, each node has 3 parts: A data item or key, a pointer to the left child and a pointer to the right child.
Preorder Traversal:
In a preorder traversal, we process/visit the root node first. Then we traverse the left subtree in a preorder manner. Finally, we visit the right subtree again in a preorder manner.
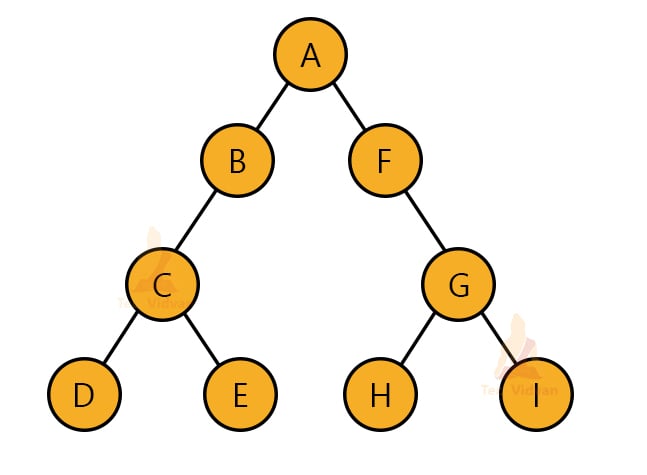
For example, consider the following tree:
Here, the root node is A. All the nodes on the left of A are a part of the left subtree whereas all the nodes on the right of A are a part of the right subtree. Thus, according to preorder traversal, we will first visit the root node, so A will print first and then move to the left subtree.
B is the root node for the left subtree. So B will print next and we will visit the left and right nodes of B. In this manner, we will traverse the whole left subtree and then move to the right subtree. Thus, the order of visiting the nodes will be: A→B→C→D→E→F→G→H→I.
Algorithm for Preorder Traversal:
for all nodes of the tree:
Step 1: Visit the root node.
Step 2: Traverse left subtree recursively.
Step 3: Traverse right subtree recursively.
Pseudo-code for Preorder Traversal:
void Preorder(struct node* ptr)
{
if(ptr != NULL)
{
printf("%d", ptr->data);
Preorder(ptr->left);
Preorder(ptr->right);
}
}
Uses of Preorder Traversal:
- If we want to create a copy of a tree, we make use of preorder traversal.
- Preorder traversal helps to give a prefix expression for the expression tree.
Inorder Traversal:
In an inorder traversal, we first visit the left subtree, then the root node and then the right subtree in an inorder manner.
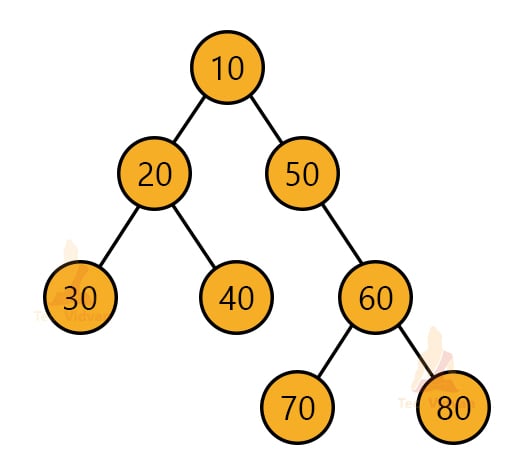
Consider the following tree:
In this case, as we visit the left subtree first, we get the node with the value 30 first, then 20 and then 40. After that, we will visit the root node and print it. Then comes the turn of the right subtree. We will traverse the right subtree in a similar manner. Thus, after performing the inorder traversal, the order of nodes will be 30→20→40→10→50→70→60→80.
Algorithm for Inorder Traversal:
for all nodes of the tree:
Step 1: Traverse left subtree recursively.
Step 2: Visit the root node.
Step 3: Traverse right subtree recursively.
Pseudo-code for Inorder Traversal:
void Inorder(struct node* ptr)
{
if(ptr != NULL)
{
Inorder(ptr->left);
printf("%d", ptr->data);
Inorder(ptr->right);
}
}
Uses of Inorder Traversal:
- Used to print the nodes of a binary search tree in non-decreasing order.
- We can also use the inorder traversal to get the non-increasing order of a BST.
Postorder Traversal:
Postorder traversal is a kind of traversal in which we first traverse the left subtree in a postorder manner, then traverse the right subtree in a postorder manner and at the end visit the root node.
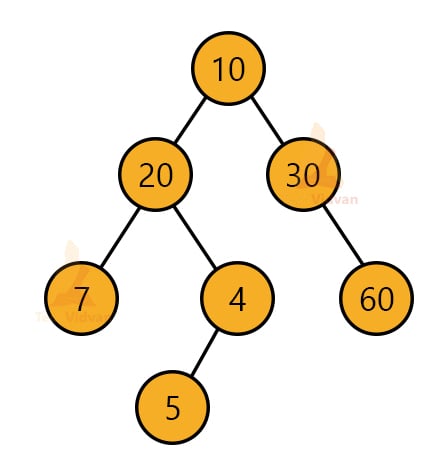
For example, in the following tree:
The postorder traversal will be 7→5→4→20→60→30→10.
Algorithm for Postorder Traversal:
for all nodes of the tree:
Step 1: Traverse left subtree recursively.
Step 2: Traverse right subtree recursively.
Step 3: Visit the root node.
Pseudo-code for Postorder Traversal:
void Postorder(struct node* ptr)
{
if(ptr != NULL)
{
Postorder(ptr->left);
Postorder(ptr->right);
printf(“%d”, ptr->data);
}
}
Uses of Postorder Traversal:
- It helps to delete the tree.
- It helps to get the postfix expression in an expression tree.
Implementation of Traversal in C:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int key;
struct Node* left;
struct node* right;
};
void inorder_traversal(struct node* root) {
if (root == NULL)
return;
inorder_traversal(root->left);
printf("%d ->", root->key);
inorder_traversal(root->right);
}
void preorder_traversal(struct node* root) {
if (root == NULL)
return;
printf("%d ->", root->key);
preorder_traversal(root->left);
preorder_traversal(root->right);
}
void postorder_traversal(struct node* root) {
if (root == NULL)
return;
postorder_traversal(root->left);
postorder_traversal(root->right);
printf("%d ->", root->key);
}
struct Node* create_node(value) {
struct Node* new_node = malloc(sizeof(struct Node));
new_node->key = value;
new_node->left = NULL;
new_node->right = NULL;
return new_node;
}
struct Node* insert_left(struct Node* root, int value) {
root->left = create_node(value);
return root->left;
}
struct Node* insert_right(struct Node* root, int value) {
root->right = create_node(value);
return root->right;
}
int main() {
struct node* root = create_node(1);
insert_left(root, 12);
insert_right(root, 9);
insert_left(root->left, 5);
insert_right(root->left, 6);
printf("Inorder traversal \n");
inorder_traversal(root);
printf("\nPreorder traversal \n");
preorder_traversal(root);
printf("\nPostorder traversal \n");
postorder_traversal(root);
}
Traversal Implementation in C++:
#include <bits/stdc++.h>
struct Node {
int key;
struct Node* left;
struct node* right;
};
void inorder_traversal(struct node* root) {
if (root == NULL)
return;
inorder_traversal(root->left);
cout << "->" << root->key;
inorder_traversal(root->right);
}
void preorder_traversal(struct node* root) {
if (root == NULL)
return;
cout << "->" << root->key;
preorder_traversal(root->left);
preorder_traversal(root->right);
}
void postorder_traversal(struct node* root) {
if (root == NULL)
return;
postorder_traversal(root->left);
postorder_traversal(root->right);
cout << "->" << root->key;
}
struct Node* create_node(value) {
struct Node* new_node = malloc(sizeof(struct Node));
new_node->key = value;
new_node->left = NULL;
new_node->right = NULL;
return new_node;
}
struct Node* insert_left(struct Node* root, int value) {
root->left = create_node(value);
return root->left;
}
struct Node* insert_right(struct Node* root, int value) {
root->right = create_node(value);
return root->right;
}
int main() {
struct node* root = create_node(1);
insert_left(root, 12);
insert_right(root, 9);
insert_left(root->left, 5);
insert_right(root->left, 6);
cout << "Inorder traversal \n";
inorder_traversal(root);
cout << "\nPreorder traversal \n";
preorder_traversal(root);
cout << "\nPostorder traversal \n";
postorder_traversal(root);
}
Implementation of traversal in Java:
class Node {
int data;
Node left, right;
public Node(int key) {
data = key;
left = right = null;
}
}
class Binary_tree {
Node root;
Binary_tree() {
root = null;
}
void postorder_traversal(Node node) {
if (node == null)
return;
postorder_traversal(node.left);
postorder_traversal(node.right);
System.out.print(node.data + "->");
}
void inorder_traversal(Node node) {
if (node == null)
return;
inorder_traversal(node.left);
System.out.print(node.data + "->");
inorder_traversal(node.right);
}
void preorder_traversal(Node node) {
if (node == null)
return;
System.out.print(node.data + "->");
preorder_traversal(node.left);
preorder_traversal(node.right);
}
public static void main(String[] args) {
Binary_tree tree = new Binary_tree();
tree.root = new Node(10);
tree.root.left = new Node(12);
tree.root.right = new Node(30);
tree.root.left.left = new Node(15);
tree.root.left.right = new Node(25);
System.out.println("Inorder traversal");
tree.inorder(tree.root);
System.out.println("\nPreorder traversal ");
tree.preorder(tree.root);
System.out.println("\nPostorder traversal");
tree.postorder(tree.root);
}
}
Implementation of traversal in Python:
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.val = data
def inorder_traversal(root):
if root:
inorder_traversal(root.left)
print(str(root.val) + "->", end='')
inorder_traversal(root.right)
def postorder_traversal(root):
if root:
postorder_traversal(root.left)
postorder_traversal(root.right)
print(str(root.val) + "->", end='')
def preorder_traversal(root):
if root:
print(str(root.val) + "->", end='')
preorder_traversal(root.left)
preorder_traversal(root.right)
root = Node(10)
root.left = Node(12)
root.right = Node(30)
root.left.left = Node(15)
root.left.right = Node(25)
print("Inorder traversal ")
inorder(root)
print("\nPreorder traversal ")
preorder(root)
print("\nPostorder traversal ")
postorder(root)
Applications of Binary Tree:
- The most important application of the binary tree is that it is used to implement the heap data structure.
- Used in compiler design to create syntax trees that help to ensure the correctness of the syntax.
- Binary trees help in accessing data easily.
- Used in computer networks to implement routing algorithms in routers.
Conclusion:
This article covers different types of traversal possible for the tree data structure. We have seen the different possible ways to visit all the nodes of a tree. Traversal is a very important operation as it is the basis of other operations. We have seen the implementation of tree traversal in different programming languages such a C, C++, Java and Python.